题目内容
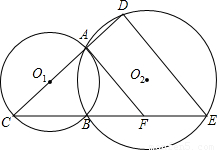
如图，已知圆O1与圆O2相交于A，B两点，直线O1A交圆O1于C，交圆O2于D，连接CB
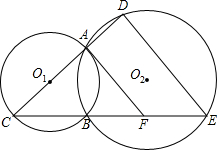
并延长交圆O2于E，AF切圆O1于A，交CE于F．
（1）求证：
=
；
（2）若
=
，圆O1的半径为2，且∠C=30°，求DE的长．
并延长交圆O2于E，AF切圆O1于A，交CE于F．
（1）求证：
| CA |
| CD |
| AF |
| DE |
（2）若
| CA |
| AD |
| 3 |
| 2 |
（1）证明：连接AB．
∵AC是直径，
∴∠CBA=90°．
又∵四边形ABED内接于⊙O2，
∴∠CBA=∠D=90°．
又∵AF切⊙O1于A点，
∴∠CAF=90°．
∴AF∥DE．
∴
| CA |
| CD |
| AF |
| DE |
（2）∵
| CA |
| AD |
| 3 |
| 2 |
又∵CA=1，
∴CD=
| 20 |
| 3 |
在Rt△CDE中，tan30°=
| DE | ||
|
∴DE=
| 20 |
| 9 |
| 3 |
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
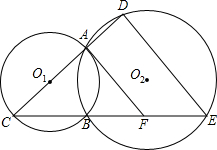并延长交圆O2于E，AF切圆O1于A，交CE于F．
；
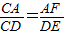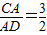，圆O1的半径为2，且∠C=30°，求DE的长．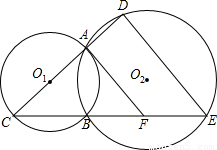
；
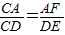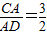，圆O1的半径为2，且∠C=30°，求DE的长．
；
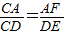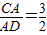，圆O1的半径为2，且∠C=30°，求DE的长．