题目内容
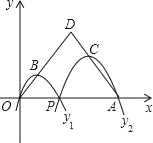
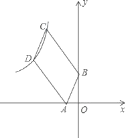
【题目】如图，已知四边形ABCD是平行四边形，BC=3AB，A，B两点的坐标分别是（﹣1，0），（0，2），C，D两点在反比例函数
（x＜0）的图象上，则k的值等于_____．
【答案】﹣24．
【解析】
设点C坐标为（a，
），根据AC与BD的中点坐标相同，可得出点D的坐标，将点D的坐标代入函数解析式可得出k关于a的表达式，再由BC＝3AB＝3
，可求出a的值，继而得出k的值．
解：设点C坐标为（a，），（a＜0），点D的坐标为（x，y）．
∵四边形ABCD是平行四边形，
∴AC与BD的中点坐标相同，
∴（a1，＋0）＝（x＋0，y＋2），
则x＝a1，y＝
，
代入
，可得：k＝2a2a2 ①；
在Rt△AOB中，AB＝
＝，
∴BC＝3AB＝3，
故BC2＝（0a）2＋（2）2＝（3）2，
整理得：a4＋k24ka＝41a2，
将①k＝2a2a2，代入后化简可得：a2＝9，
∵a＜0，
∴a＝3，
∴k＝618＝24．
故答案为：24．
练习册系列答案
每课必练系列答案
相关题目
