题目内容
在平面直角坐标系中,抛物线y=ax2+bx+2与x轴交于点A(x1,0),B(x2,0)(x1<x2),且x1,x2是方程x2-2x-3=0的两个实数根,点C为抛物线与y轴的交点.
(1)求点A,B的坐标;
(2)分别求出抛物线和直线AC的解析式;
(3)若将过点(0,2)且平行于x轴的直线定义为直线y=2.设动直线y=m(0<m<2)与线段AC、BC分别交于D、E两点.在x轴上是否存在
 点P,使得△DEP为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
点P,使得△DEP为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
分析:(1)由于抛物线y=ax2+bx+2与x轴交于点A(x1,0),B(x2,0)(x1<x2),且x1,x2是方程x2-2x-3=0的两个实数根,那么解方程x2-2x-3=0即可得到点A,B的坐标;
(2)首先把A,B两点的坐标分别代入y=ax2+bx+2可以得到关于a、b的方程组,解方程组即可求出a、b的值,同时可以得到c的值,最后利用待定系数法即可求出直线AC的解析式;
(3)假设存在满足条件的点P,并设直线y=m与y轴的交点为F(0,m).
①当DE为腰时,分别过点D,E作DP1⊥x轴于P1,作EP2⊥x轴于P2,如图1,则△P1DE和△P2ED都是等腰直角三角形,然后证明△CDE∽△CAB,接着利用相似三角形的性质求出m,然后求出点D的纵坐标,也就求出了P的坐标;
②如图2,当DE为底边时,过DE的中点G作GP3⊥x轴于点P3.同样的方法可以求出D的纵坐标,也就求出了P的坐标.
(2)首先把A,B两点的坐标分别代入y=ax2+bx+2可以得到关于a、b的方程组,解方程组即可求出a、b的值,同时可以得到c的值,最后利用待定系数法即可求出直线AC的解析式;
(3)假设存在满足条件的点P,并设直线y=m与y轴的交点为F(0,m).
①当DE为腰时,分别过点D,E作DP1⊥x轴于P1,作EP2⊥x轴于P2,如图1,则△P1DE和△P2ED都是等腰直角三角形,然后证明△CDE∽△CAB,接着利用相似三角形的性质求出m,然后求出点D的纵坐标,也就求出了P的坐标;
②如图2,当DE为底边时,过DE的中点G作GP3⊥x轴于点P3.同样的方法可以求出D的纵坐标,也就求出了P的坐标.
解答:解:(1)由x2-2x-3=0,得x=-1或x=3.
∵x1<x2,
∴x1=-1,x2=3,
∴A(-1,0),B(3,0);
(2)把A,B两点的坐标分别代入y=ax2+bx+2联立求解,
得a=-
,b=
.(2分)
∴此抛物线的解析式为y=-
x2+
x+2.
∵当x=0时,y=2,
∴C(0,2).
设AC的解析式为y=kx+n(k≠0),把A,C两点坐标分别代入y=kx+n,
联立求得k=2,n=2.
∴直线AC的解析式为y=2x+2;
(3)假设存在满足条件的点P,并设直线y=m与y轴的交点为F(0,m)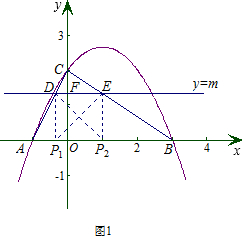
①当DE为腰时,分别过点D,E作DP1⊥x轴于P1,作EP2⊥x轴于P2,如图1,则△P1DE和△P2ED都是等腰直角三角形,
∴DE=DP1=FO=EP2=m.
∵AB=x2-x1=4,
又∵DE∥AB,
∴△CDE∽△CAB,
∴
=
,即
=
.
解得m=
.
∴点D的纵坐标是
.
∵点D在直线AC上,
∴2x+2=
,
解得x=-
,
∴D(-
,
).
∴P1(-
,0).
同理可求P2(1,0).
②如图2,当DE为底边时,过DE的中点G作GP3⊥x轴于点P3
∵P3D=P3E,∠DP3E=90°,
∴DG=EG=GP3=m,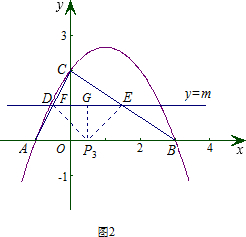
由△CDE∽△CAB,
得
=
,即
=
,
解得m=1.
同①方法求得D(-
,1),E(
,1),
∴DG=EG=GP3=1.
∴OP3=FG=FE-EG=
,
∴P3(
,0).
综上所述,满足条件的点P共有3个,
即P1(-
,0),P2(1,0),P3(
,0).
如有其他解(证)法,请酌情给分.
∵x1<x2,
∴x1=-1,x2=3,
∴A(-1,0),B(3,0);
(2)把A,B两点的坐标分别代入y=ax2+bx+2联立求解,
得a=-
| 2 |
| 3 |
| 4 |
| 3 |
∴此抛物线的解析式为y=-
| 2 |
| 3 |
| 4 |
| 3 |
∵当x=0时,y=2,
∴C(0,2).
设AC的解析式为y=kx+n(k≠0),把A,C两点坐标分别代入y=kx+n,
联立求得k=2,n=2.
∴直线AC的解析式为y=2x+2;
(3)假设存在满足条件的点P,并设直线y=m与y轴的交点为F(0,m)

①当DE为腰时,分别过点D,E作DP1⊥x轴于P1,作EP2⊥x轴于P2,如图1,则△P1DE和△P2ED都是等腰直角三角形,
∴DE=DP1=FO=EP2=m.
∵AB=x2-x1=4,
又∵DE∥AB,
∴△CDE∽△CAB,
∴
| DE |
| AB |
| CF |
| OC |
| m |
| 4 |
| 2-m |
| 2 |
解得m=
| 4 |
| 3 |
∴点D的纵坐标是
| 4 |
| 3 |
∵点D在直线AC上,
∴2x+2=
| 4 |
| 3 |
解得x=-
| 1 |
| 3 |
∴D(-
| 1 |
| 3 |
| 4 |
| 3 |
∴P1(-
| 1 |
| 3 |
同理可求P2(1,0).
②如图2,当DE为底边时,过DE的中点G作GP3⊥x轴于点P3
∵P3D=P3E,∠DP3E=90°,
∴DG=EG=GP3=m,

由△CDE∽△CAB,
得
| DE |
| AB |
| CF |
| OC |
| 2m |
| 4 |
| 2-m |
| 2 |
解得m=1.
同①方法求得D(-
| 1 |
| 2 |
| 3 |
| 2 |
∴DG=EG=GP3=1.
∴OP3=FG=FE-EG=
| 1 |
| 2 |
∴P3(
| 1 |
| 2 |
综上所述,满足条件的点P共有3个,
即P1(-
| 1 |
| 3 |
| 1 |
| 2 |
如有其他解(证)法,请酌情给分.
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和相似三角形的性质与判定及待定系数法确定函数的解析式.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.