题目内容
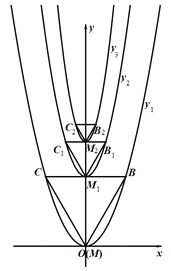
【题目】如图，抛物线
（a>0）的顶点为M，若△MCB为等边三角形，且点C，B在抛物线上，我们把这种抛物线称为“完美抛物线”，已知点M与点O重合，BC=2．
（1）求过点O、B、C三点完美抛物线
的解析式；
（2）若依次在y轴上取点M1、M2、…Mn分别作等边三角形及完美抛物线
、
、…
，其中等边三角形的相似比都是2:1，如图,n为正整数．
①则完美抛物线
= ，完美抛物线
= ；
完美抛物线
= ；
②直接写出Bn的坐标；
③判断点B1、B2、…、Bn是否在同一直线，若在，求出直线的解析式，若不在同一直线上，说明理由．
【答案】（1）
；（2）①
， 
， 
；②（ 
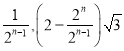）；③在， 
.
【解析】解：（1）根据题意得B的坐标为（1， 
），设抛物线的解析式是
，
代入得
，所以
.
（2）①
、
，
.
②（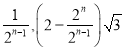
）.
③
.
练习册系列答案
阅读快车系列答案
相关题目