题目内容
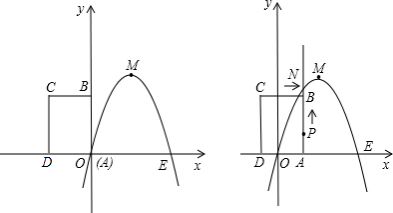
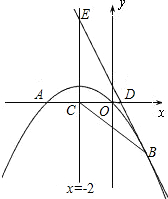
如图,已知抛物线 经过点
经过点 ,抛物线的顶点为
,抛物线的顶点为 ,过
,过 作射线
作射线 .过顶点
.过顶点 平行于
平行于 轴的直线交射线
轴的直线交射线 于点
于点 ,
, 在
在 轴正半轴上,连结
轴正半轴上,连结 .
.
【小题1】求该抛物线的解析式;
【小题2】动点 从点
从点 出发,以每秒1个长度单位的速度沿射线
出发,以每秒1个长度单位的速度沿射线 运动,设点
运动,设点 运动的时间为
运动的时间为 .问当
.问当 为何值时,四边形
为何值时,四边形 分别为平行四边形?直角梯形?等腰梯形?
分别为平行四边形?直角梯形?等腰梯形?
【小题3】若 ,动点
,动点 和动点
和动点 分别从点
分别从点 和点
和点 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿
同时出发,分别以每秒1个长度单位和2个长度单位的速度沿 和
和 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为
运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为
 ,连接
,连接 ,当
,当 为何值时,四边形
为何值时,四边形 的面积最小?并求出最小值及此时
的面积最小?并求出最小值及此时 的长.
的长.
【小题1】)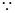 抛物线
抛物线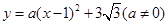 经过点
经过点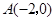 ,
,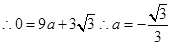
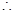 二次函数的解析式为:
二次函数的解析式为: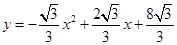
【小题2】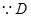 为抛物线的顶点
为抛物线的顶点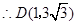 过
过 作
作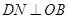 于
于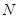 ,则
,则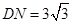 ,
,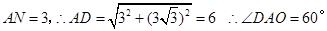
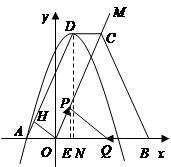
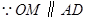
 当
当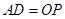 时,四边形
时,四边形 是平行四边形
是平行四边形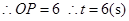
 当
当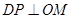 时,四边形
时,四边形 是直角梯形
是直角梯形
过 作
作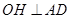 于
于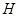 ,
,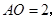 则
则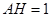
(如果没求出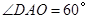 可由
可由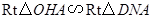 求
求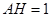 )
)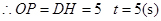
 当
当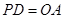 时,四边形
时,四边形 是等腰梯形
是等腰梯形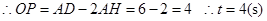 综上所述:当
综上所述:当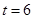 、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形.
、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形.
【小题3】由(2)及已知,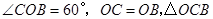 是等边三角形
是等边三角形
则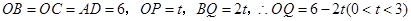
过 作
作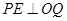 于
于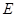 ,则
,则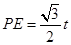 ····················· 1分
····················· 1分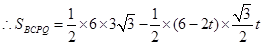 =
=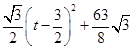
当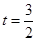 时,
时,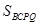 的面积最小值为
的面积最小值为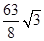
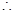 此时
此时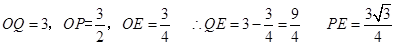
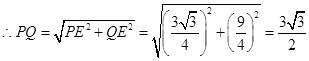
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.
2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E, 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),