题目内容
如图, 中,
中, ,
, 是
是 的中点,∠
的中点,∠ =90°,
=90°, ,
, ,垂足分别为
,垂足分别为 .试说明四边形
.试说明四边形 是正方形.
是正方形.
 中,
中, ,
, 是
是 的中点,∠
的中点,∠ =90°,
=90°, ,
, ,垂足分别为
,垂足分别为 .试说明四边形
.试说明四边形 是正方形.
是正方形.
见解析
试题分析:先由∠
 =90°,
=90°, ,
, 证得四边形AEDF是矩形,再由
证得四边形AEDF是矩形,再由 可得∠B=∠C,结合
可得∠B=∠C,结合 是
是 的中点,可得△BDE≌△CDF,得到DE=DF,即可证得结论.
的中点,可得△BDE≌△CDF,得到DE=DF,即可证得结论.∵∠
 =90°,
=90°, ,
,
∴四边形AEDF是矩形
∵
 ,
,∴∠B=∠C
∵因为
 是
是 的中点,
的中点, ∴BD=DC
∵
 ,
,
∴△BDE≌△CDF
∴DE=DF
∴矩形AEDF是正方形.
点评:解答本题的关键是熟记有三个角是直角的四边形的矩形,邻边相等的矩形是正方形.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目

 轴上移动.小明同学写出了两个使△POE为等腰三角形的P点坐标(
轴上移动.小明同学写出了两个使△POE为等腰三角形的P点坐标( ,
, )和(
)和( ,
,


 中,
中, 是
是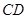 边上的中点,
边上的中点, 与
与 相交于点
相交于点 ,连接
,连接 .(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角).
.(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角). 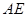 试判断
试判断 于点
于点 ,试判断
,试判断 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.