题目内容
如图, 为正比例函数
为正比例函数 图象上的一个动点,
图象上的一个动点, 的半径为
的半径为 ,设点
,设点 的坐标为
的坐标为 .
.

(1)求 与直线
与直线 相切时点
相切时点 的坐标.(4分)
的坐标.(4分)
(2)请直接写出 与直线
与直线 相交、相离时
相交、相离时 的取值范围.(3分)
的取值范围.(3分)
【答案】
(1)点 的坐标为
的坐标为 或
或 (2)当
(2)当 时,
时, 与直线
与直线 相交.当
相交.当 或
或 时,
时, 与直线
与直线 相离
相离
【解析】(1)过 作直线
作直线 的垂线,垂足为
的垂线,垂足为 .
.
当点 在直线
在直线 右侧时,
右侧时, ,得
,得 ,
, . (2分)
. (2分)
当点 在直线
在直线 左侧时,
左侧时, ,得
,得 ,
, . (4分)
. (4分)
 当
当 与直线
与直线 相切时,点
相切时,点 的坐标为
的坐标为 或
或 .
.
(2)当 时,
时, 与直线
与直线 相交.
相交.
当 或
或 时,
时, 与直线
与直线 相离
相离
(1)根据直线和圆相切应满足圆心到直线的距离等于半径,首先求得点P的横坐标,再根据直线的解析式求得点P的纵坐标.
(2)根据(1)的结论,即可分析出相离和相交时x的取值范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
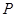 为正比例函数
为正比例函数 图象上的一个动点,
图象上的一个动点, 的半径为
的半径为 ,设点
,设点 .
.
 相切时点
相切时点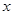 的取值范围.(3分)
的取值范围.(3分) 为正比例函数
为正比例函数 图象上的一个动点,⊙P的半径为
图象上的一个动点,⊙P的半径为 ,当⊙P与直线
,当⊙P与直线 相切时,则点
相切时,则点

 为正比例函数
为正比例函数 图象上的一个动点,⊙P的半径为
图象上的一个动点,⊙P的半径为 ,当⊙P与直线
,当⊙P与直线 相切时,则点
相切时,则点