题目内容
 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2
将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
分析:根据直角三角形30°角所对的直角边等于斜边的一半求出BC,再利用勾股定理列式求出AC,过点D作DF⊥AC于F,根据等腰直角三角形的性质求出DF=CF=
AC,设CE=x,表示出EF,然后分别用勾股定理表示出DE2、BE2,再列出方程求解即可.
| 1 |
| 2 |
解答: 解:∵AB=2
解:∵AB=2
,∠BAC=30°,
∴BC=
AB=
×2
=
,
根据勾股定理,AC=
=
=3,
过点D作DF⊥AC于F,
∵△ACD是等腰直角三角形,
∴DF=CF=
AC=
,
设CE=x,则EF=
-x,
在Rt△DEF中,DE2=DF2+EF2=(
)2+(
-x)2,
在Rt△BCE中,BE2=BC2+CE2=(
)2+x2,
∵DE=BE,
∴(
)2+(
-x)2=(
)2+x2,
解得x=
,
所以,AE=AC-CE=3-
=
.
故答案为:
.
 解:∵AB=2
解:∵AB=2| 3 |
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
根据勾股定理,AC=
| AB2-BC2 |
(2
|
过点D作DF⊥AC于F,
∵△ACD是等腰直角三角形,
∴DF=CF=
| 1 |
| 2 |
| 3 |
| 2 |
设CE=x,则EF=
| 3 |
| 2 |
在Rt△DEF中,DE2=DF2+EF2=(
| 3 |
| 2 |
| 3 |
| 2 |
在Rt△BCE中,BE2=BC2+CE2=(
| 3 |
∵DE=BE,
∴(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解得x=
| 1 |
| 2 |
所以,AE=AC-CE=3-
| 1 |
| 2 |
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题考查了勾股定理的应用,直角三角形30°角所对的直角边等于斜边的一半的性质,等腰直角三角形的性质,作辅助线,利用勾股定理表示出DE、BE然后列出方程是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
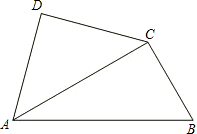 尺(△ACD)的斜边恰好重合.已知AB=
尺(△ACD)的斜边恰好重合.已知AB=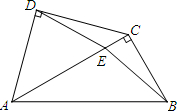 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2
将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2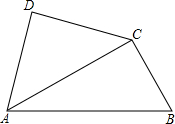 ACD)的斜边恰好重合.已知AB=2
ACD)的斜边恰好重合.已知AB=2
