Question

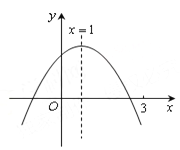
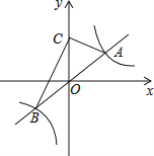
【题目】如图，反比例函数y=（k＞0）的图象与一次函数y=x的图象交于A、B两点（点A在第一象限）．

（1）当点A的横坐标为4时．

①求k的值；

②根据反比例函数的图象，直接写出当-4＜x＜1（x≠0）时，y的取值范围；

（2）点C为y轴正半轴上一点，∠ACB=90°，且△ACB的面积为10，求k的值．

Answer 1

【答案】（1）①12，②y＜-3或y＞12；（2）6

【解析】

（1）①根据点A的横坐标是4，可以求得点A的纵坐标，从而可以求得k的值；

②根据反比例函数的性质，可以写出y的取值范围；

（2）根据点C为y轴正半轴上一点，∠ACB=90°，且△ACB的面积为10，灵活变化，可以求得点A的坐标，从而可以求得k的值．

解：（1）①将x=4代入y=x得，y=3，

∴点A（4，3），

∵反比例函数y=（k＞0）的图象与一次函数y=x的图象交于A点，

∴3=，

∴k=12；

②∵x=-4时，y==-3，x=1时，y==12，

∴由反比例函数的性质可知，当-4＜x＜1（x≠0）时，y的取值范围是y＜-3或y＞12；

（2）设点A为（a，），

则OA==，

∵点C为y轴正半轴上一点，∠ACB=90°，且△ACB的面积为10，

∴OA=OB=OC=，

∴S△ACB==10，

解得，a=，

∴点A为（2，），

∴=，

解得，k=6，

即k的值是6．