题目内容
6.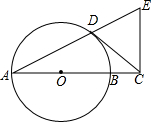 已知AB为⊙O的直径,点D为⊙O上一点,过点D作⊙O的切线,交AB的延长线于点C,过点C作AC的垂线,交AD的延长线于点E
已知AB为⊙O的直径,点D为⊙O上一点,过点D作⊙O的切线,交AB的延长线于点C,过点C作AC的垂线,交AD的延长线于点E(1)证明:△CDE为等腰三角形;
(2)若AD=2,$\frac{BC}{CE}$=$\frac{1}{2}$,求⊙O的面积.
分析 (1)连接OD,利用等角的余角相等证明∠E=∠EDC即可.
(2)作OF⊥AE于F,连接BD,设BC=a,则EC=CD=2a,由CD2=CB•CA,得CA=4a,AB=3a,由△AFO∽△ACE求出OF,在RT△AFO中求出AO即可.
解答 (1)证明:如图,连接OD,
∵CD是⊙O切线,
∴OD⊥CD,
∴∠ODC=90°,
∴∠EDC+∠ADO=90°,
∵∠ACB=90°,∠A+∠E=90°,
∵OA=OD,
∴∠A=∠ADO,
∴∠E=∠EDC,
∴CD=CE,
∴△CDE是等腰三角形.
(2)作OF⊥AE于F,连接BD,设BC=a,则EC=CD=2a,
∵AD=2,OF⊥AD,
∴AF=DF=1,
∵CD2=CB•CA,
∴4a2=a•AC,
∴AC=4a,AB=3a,
∵∠A=∠A,∠AFO=∠ACE,
∴△AFO∽△ACE,
∴$\frac{AF}{AC}$=$\frac{OF}{EC}$,
∴$\frac{1}{4a}=\frac{OF}{2a}$,
∴OF=$\frac{1}{2}$,
∴AO=$\sqrt{A{F}^{2}+O{F}^{2}}$=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$,
⊙O的面积为$\frac{5π}{4}$.
点评 本题考查切线的性质、等腰三角形的判定、相似三角形的判定和性质、勾股定理等知识,解题的关键是切线性质的应用,记住圆中常用辅助线(弦心距),学会转化的思想,在解题时设未知数是常用的手段,属于中考常考题型.

练习册系列答案
相关题目
14.下列事件是必然事件的是( )
| A. | 太阳从西方升起 | B. | 打开电视正在播放《新闻联播》 | ||
| C. | 若a≤0,则|a|=-a | D. | 某运动员投篮时连续3次全中 |
18.一元二次方程2x2-5x-7=0的二次项系数、一次项系数、常数项分别是( )
| A. | 5;2;7 | B. | 2;-5;-7 | C. | 2;5;-7 | D. | -2;5;7 |
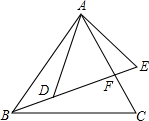 如图,点B、D、E在一条直线上,BE与AC相交于点F,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,若∠EAC=18°,则∠EBC=18°.
如图,点B、D、E在一条直线上,BE与AC相交于点F,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,若∠EAC=18°,则∠EBC=18°.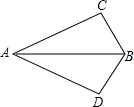 如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要加条件BC=BD或AC=AD.
如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要加条件BC=BD或AC=AD.