Question

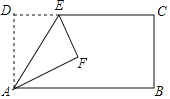
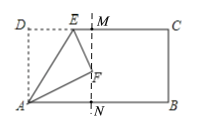
【题目】如图，矩形ABCD中，AD＝20，AB＝32，点E为DC上一个动点，把△ADE沿AE折叠，当点D的对应点F落在矩形ABCD的对称轴上时，则DE的长为_____

Answer 1

【答案】10或．

【解析】

过点F作MN⊥AB于点N，MN交CD于点M，如图，由矩形有两条对称轴可知要分两种情况考虑，根据折叠的特性可找出各边的关系，然后在Rt△AFN与Rt△EMF中，利用勾股定理得出关于DE长度的方程，解方程即可得出结果．

解：过点F作MN⊥AB于点N，MN交CD于点M，如图所示．

设DE=a，则EF=a．

∵矩形有两条对称轴，∴分两种情况考虑：

①当DM＝CM时，AN＝DM＝CD＝AB＝16，AD＝AF＝20，

在Rt△AFN中，由勾股定理可知：NF＝＝12，

∴MF＝MN﹣NF＝AD﹣NF＝8，EM＝DM﹣DE＝16﹣a，

∵EF2＝EM2+MF2，即a2＝（16﹣a）2+64，

解得：a＝10；

②当MF＝NF时，MF＝NF＝MN＝AD＝10，

在Rt△AFN中，由勾股定理可知：AN＝＝10，

∴EM＝DM﹣DE＝AN﹣DE＝10﹣a，

∵EF2＝EM2+MF2，即a2＝（10﹣a）2+102，

解得：a＝．

综上知：DE＝10或．

故答案为：10或．