题目内容
已知a，b是两个任意有理数，且a＜b，问是否存在无理数α，使得a＜α＜b成立？
解：∵a＜b，
-1＞0，
∴
，
即
①
又∵a＜b=b+
，
∴a+b-b
b，
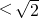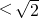即（-1）b+ab ②
由①，②有
，
∴
，
取
=b+
，
∵b，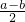
是有理数，且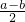≠0，
∴b+是无理数，
即存在无理数α，使得a＜α＜b成立．
分析：在a＜b的左右两边同乘以-1，整理得出①，（-1）b+a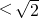b ②，由①，②得出，从而讨论α的取值．
点评：此题难度较大，主要考查实数的运算，同时应用了不等式的性质等．
-1＞0，∴
，即
①又∵a＜b=b+
，∴a+
b-bb，即（
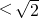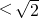-1）b+ab ②由①，②有
，∴
，取
=b+，∵b，
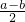是有理数，且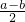≠0，∴b+
是无理数，即存在无理数α，使得a＜α＜b成立．
分析：在a＜b的左右两边同乘以
-1，整理得出①，（-1）b+a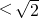b ②，由①，②得出，从而讨论α的取值．点评：此题难度较大，主要考查实数的运算，同时应用了不等式的性质等．
练习册系列答案
相关题目
)．
）是两个任意质数，那么下列四个分式：①
；②
；③
；④
中，总是最简分式的有（ ）
（
＞
）是两个任意质数，那么下列四个分数
； ②
； ③
； ④
中，总是最简分数的有