题目内容
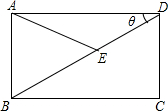如图，矩形ABCD（AD＞AB）中AB=a，∠BDA=θ，作AE交BD于E，且AE=AB，试用a与θ表示：AD=分析：（1）根据直角三角形中锐角三角函数的定义解答．
（2）过点A作AN⊥BD于N，根据等腰三角形的性质及锐角三角函数的定义解答．
（2）过点A作AN⊥BD于N，根据等腰三角形的性质及锐角三角函数的定义解答．
解答：
解：∵在直角△ABD中，tan=
，
∴AD=
=
；
过点A作AN⊥BD于N．
∵AB=AE，∴BE=2BN．
∵∠BAN+∠ABN=90°，∠ABN+∠θ=90°，
∴∠BAN=∠θ，
∴BE=2BN=2AB•sinθ=2a•sinθ．
解：∵在直角△ABD中，tan=| AB |
| AD |
∴AD=
| AB |
| tanθ |
| a |
| tanθ |
过点A作AN⊥BD于N．
∵AB=AE，∴BE=2BN．
∵∠BAN+∠ABN=90°，∠ABN+∠θ=90°，
∴∠BAN=∠θ，
∴BE=2BN=2AB•sinθ=2a•sinθ．
点评：本题主要考查了余切函数、正弦函数的定义，并运用了等腰三角形的三线合一定理，是需要识记的内容．
练习册系列答案
小学课时作业全通练案系列答案
相关题目
17、已知，如图，矩形ABCD中，AC与BD相交于点O，BE⊥AC于E，CF⊥BD于F．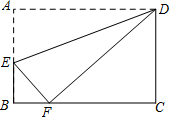
（2012•武汉）如图，矩形ABCD中，点E在边AB上，将矩形ABCD沿直线DE折叠，点A恰好落在边BC的点F处．若AE=5，BF=3，则CD的长是（ ）
Q的面积为y（cm2）．
如图，矩形ABCD的边AB、BC的长分别为