题目内容
如图:抛物线 与x 轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C。
与x 轴交于A、B两点,点A的坐标是(1,0),与y轴交于点C。⑴求抛物线的对称轴和点B的坐标;
⑵过点C作CP⊥对称轴于点P,连结BC交对称轴于点D,连结AC、BP,且
 ,求抛物线的解析式;
,求抛物线的解析式;⑶在⑵的条件下,设抛物线的顶点为G,连结BG、CG、求
 BCG的面积。
BCG的面积。
⑴对称轴是x=- …………………2′
…………………2′
∵点A(1,0)且点A、B关于x=2对称
∴点B(3,0) …………4′
⑵点A(1,0),B(3,0)
∴ AB=2
∵ CP⊥对称轴于P
∴ CP∥AB
∵ 对称轴是x=2
∴ AB∥CP且AB=CP
∴ 四边形ABPC是平行四边形 …5′
设点C(0,x) x<0
在Rt AOC中,AC=
AOC中,AC=
∴ BP=
在Rt BOC中,BC=
BOC中,BC=
∵
∴ BD=

∵ ∠BPD=∠PCB 且∠PBD=∠CBP
∴ BPD~
BPD~ BCP …………………7′
BCP …………………7′
∴
即

∴

∵ 点C在y轴的负半轴上 ∴ 点C(0, )…8′
)…8′
∴
∵ 过点(1,0)
∴


解析式是: …………………9′
…………………9′
⑶ 当x=2时,
顶点坐标G是(2, ) …………………10′
) …………………10′
设CG的解析式是:
(0, )(2,
)(2, )
)
∴
∴ …………………11′
…………………11′
设CG与x轴的交点为H
令y="0 " 则 得
得 
即H( ,0) …………………12′
,0) …………………12′
∴ BH= =
=




 …………………13′
…………………13′
(本题若有其它解法,正确给满分)解析:
略
 …………………2′
…………………2′∵点A(1,0)且点A、B关于x=2对称
∴点B(3,0) …………4′
⑵点A(1,0),B(3,0)
∴ AB=2
∵ CP⊥对称轴于P
∴ CP∥AB
∵ 对称轴是x=2
∴ AB∥CP且AB=CP
∴ 四边形ABPC是平行四边形 …5′
设点C(0,x) x<0
在Rt
 AOC中,AC=
AOC中,AC=
∴ BP=

在Rt
 BOC中,BC=
BOC中,BC=
∵

∴ BD=


∵ ∠BPD=∠PCB 且∠PBD=∠CBP
∴
 BPD~
BPD~ BCP …………………7′
BCP …………………7′∴

即


∴


∵ 点C在y轴的负半轴上 ∴ 点C(0,
 )…8′
)…8′∴

∵ 过点(1,0)
∴



解析式是:
 …………………9′
…………………9′⑶ 当x=2时,

顶点坐标G是(2,
 ) …………………10′
) …………………10′设CG的解析式是:

(0,
 )(2,
)(2, )
)∴

∴
 …………………11′
…………………11′设CG与x轴的交点为H
令y="0 " 则
 得
得 
即H(
 ,0) …………………12′
,0) …………………12′∴ BH=
 =
=




 …………………13′
…………………13′(本题若有其它解法,正确给满分)解析:
略

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
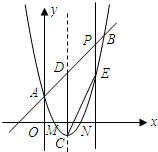 作x轴的垂线交抛物线于点E,使四边形DCEP为平行四边形?若存在,请求出该平行四边形的面积;若不存在,说明理由.
作x轴的垂线交抛物线于点E,使四边形DCEP为平行四边形?若存在,请求出该平行四边形的面积;若不存在,说明理由.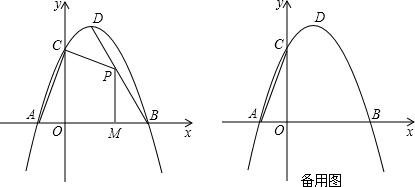
 (2013•营口)如图,抛物线与x轴交于A(1,0)、B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
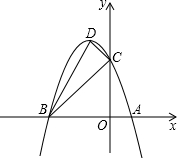
(2013•营口)如图,抛物线与x轴交于A(1,0)、B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D. 如图,抛物线与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C(0,-4).