Question

如图，直线AB经过圆心O，△BCT内接于⊙O，B是

TC

的中点，连接AT，且TB平分锐角∠CTA，cos∠CTA=

1

2

．
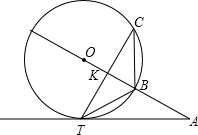
（1）求证：AT是⊙O的切线；
（2）若CT交OA于K，BC=2，请你猜测AT的长度，并证明你的结论．

Answer 1

分析：（1）连接OT，由BT是∠ATC的角平分线，cos∠CTA=

1

2

，可求∠ATB=∠BTC=30°，而B是弧CT的中点，那么∠C=30°，利用圆周角定理可求∠BOT=60°，而OB=OT，则△BOT是等边三角形，则∠OTB=60°，那么可求∠ATO=90°，即AT是⊙O的切线；
（2）由于OT⊥AT，∠BOT=60°，则∠A=30°，那么在△ATB和△CTB中，∠A=∠C，∠ATB=∠CTB，BT=BT，利用AAS可证△ATB≌△CTB，从而有AT=CT，在Rt△BCK中，由于BC=2，∠C=30°，易求CK=cos30°×BC=

3

，即CT=2

3

，那么AT=2

3

．

解答：证明：（1）∵TB平分锐角∠CTA，且cos∠CTA=

1

2

，
∴∠CTB=∠BTA=30°，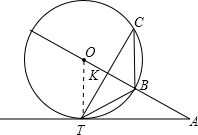
又∵B是

TC

的中点，
∴∠C=∠CTB=30°，
连接OT，
则∠TOB=

TB

=2∠C=60°，又OT=OB，
∴△BOT是等边三角形，
∴∠OTB=60°，
∴∠OTA=∠OTB+∠BTA=90°，
即：OT⊥AT，
∴AT是⊙O的切线；

（2）猜想：AT=2

3

，
理由：∵OT⊥AT，∠TOB=60°，
∴∠A=30°=∠C，
又∵∠CTB=∠BTA且TB=TB，
∴△CBT≌△ABT，
∴AT=CT，
在Rt△BCK中，CK=cos30°×CB=

3

，
∴CT=2

3

，
∴AT的长度为2

3

．

点评：本题利用了角平分线定义、三角函数值、等边三角形的判定和性质、同圆中等弧所对的圆周角相等、圆周角定理、全等三角形的判定和性质、垂径定理．