题目内容
已知△ABC的三个内角满足：∠A：∠B：∠C=1：2：3，则这是一个
- A.锐角三角形
- B.直角三角形
- C.钝角三角形
- D.无法确定
B
分析：根据比例设∠A、∠B、∠C分别为k、2k、3k，然后根据三角形内角和定理列式进行计算求出k值，再求出最大的角∠C即可得解．
解答：设∠A、∠B、∠C分别为k、2k、3k，
则k+2k+3k=180°，
解得k=30°，
所以，最大的角∠C=3×30°=90°，
所以，这个三角形是直角三角形．
故选B．
点评：本题考查了三角形的内角和定理，利用“设k法”求解更加简便．
分析：根据比例设∠A、∠B、∠C分别为k、2k、3k，然后根据三角形内角和定理列式进行计算求出k值，再求出最大的角∠C即可得解．
解答：设∠A、∠B、∠C分别为k、2k、3k，
则k+2k+3k=180°，
解得k=30°，
所以，最大的角∠C=3×30°=90°，
所以，这个三角形是直角三角形．
故选B．
点评：本题考查了三角形的内角和定理，利用“设k法”求解更加简便．
练习册系列答案
相关题目
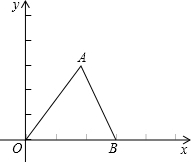如图，在平面直角坐标系中，已知：△ABC的三个顶点的坐标分别是A（4，6）、B（0，0）、C（6，0）．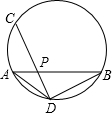
23、已知△ABC在坐标平面内三顶点的坐标分别为A（0，2）、B（3，3）、C（2，1）．以B为位似中心，画出△Α1Β1С1与△ABC相似（与图形同向），且相似比是2的三角形，它的三个对应顶点的坐标分别是：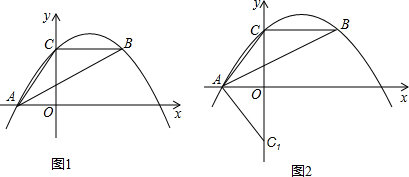
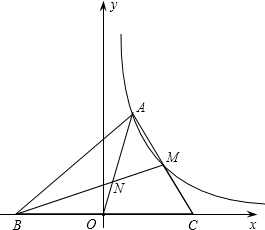标分别是A（1，2