题目内容
已知
，则x3y+xy3= ．
10 ．
【考点】二次根式的化简求值．
【专题】计算题．
【分析】由已知得x+y=2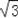
，xy=1，把x3y+xy3分解因式再代入计算．
【解答】解：∵
，
∴x+y=2
，xy=1，
∴x3y+xy3=xy（x2+y2）
=xy[（x+y）2﹣2xy]
=（2）2﹣2
=10．
【点评】解题时注意，灵活应用二次根式的乘除法法则，切忌把x、y直接代入求值．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
=
，求
的值．
有意义的x的取值范围是 ．
B．
__________﹣
．
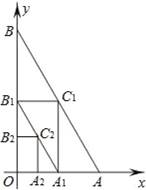
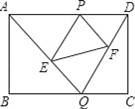