��Ŀ����
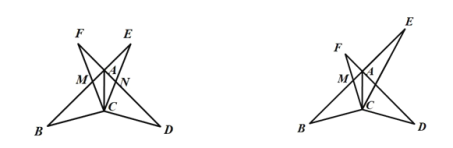
����Ŀ����ͼ���ڡ�ABC�У�AB��BC����B��90�㣬��DΪ�߶�BC��һ�����㣨�����B��C�غϣ�������AD�����߶�AD�Ƶ�D˳ʱ����ת90��õ��߶�DE������EC.
��1���������ⲹȫͼ1��
����֤����EDC����BAD;
��2����С��ͨ���۲졢ʵ�飬������룺�ڵ�D�˶��Ĺ����У��߶�CE��BD��������ϵʼ�ղ��䣬�õ�ʽ��ʾΪ�� ����
��С�������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1������E��EF��BC����BC�ӳ����ڵ�F��ֻ��֤��ADB�ա�DEF��
�뷨2�����߶�AB��ȡһ��F��ʹ��BF��BD������DF��ֻ��֤��ADF�ա�DEC��
�뷨3���ӳ�AB��F��ʹ��BF��BD������DF��CF��ֻ��֤�ı���DFCEΪƽ���ı��Σ�
����
����ο�������뷨������С��֤��(2)���еIJ��룮��һ�ַ������ɣ�
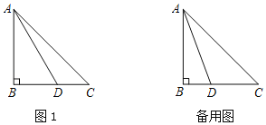
���𰸡���1���ټ������ڼ�������2���ٲ��룺CE��![]() BD�ڼ�����
BD�ڼ�����
��������
��1���������ⲹȫͼ�μ��ɣ����ɽǵĹ�ϵ���ɵó����ۣ�
��2������ȫ�������κ��ɶ����ɲ���CE=![]() BD��
BD��
���뷨1������E��EF��BC����BC�ӳ����ڵ�F��֤����ADB�ա�DEF���ó�AB=DF��BD=EF��֤��CF=BD=EF���ó���CEF�ǵ���ֱ�������Σ����ɵó����ۣ�
�뷨2�����߶�AB��ȡһ��F��ʹ��BF=BD������DF��֤��AF=DC��֤����ADF�ա�DEC���ó�CE=DF=![]() BD���ɣ�
BD���ɣ�
�뷨3���ӳ�AB��F��ʹ��BF=BD������DF��CF��֤����ABD�ա�CBF���ó�AD=CF����BAD=��BCF����֤���ı���DFCEΪƽ���ı��Σ����ɵó����ۣ�
��1������ȫ��ͼ����ͼ1��ʾ��

�ڡߡ�ADE����B��90�������EDC+��ADB����BAD+��ADB��90����
���EDC����BAD��
��2�������룺CE��![]() BD��
BD��
�ʴ�Ϊ��CE��![]() BD��
BD��
���뷨1��
֤��������E��EF��BC����BC�ӳ����ڵ�F����ͼ2��ʾ��
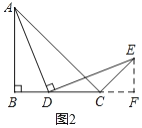
���F��90�������B����F��
����ADB����DEF��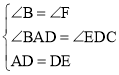 ��
��
���ADB�ա�DEF��AAS������AB��DF��BD��EF��
��AB��BC����DF��BC����DC+CF��BD+DC��
��CF��BD��EF�����CEF�ǵ���ֱ�������Σ�
��CE��![]() CF��
CF��![]() BD��
BD��
�뷨2��
֤�������߶�AB��ȡһ��F��ʹ��BF��BD������DF����ͼ3��ʾ��
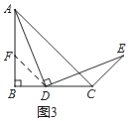
�ߡ�B��90����AB��BC��
��DF��![]() BD��
BD��
��AB��BC��BF��BD��
��AB��BF��BC��BD��
��AF��DC��
����ADF����DEC��
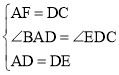 ��
��
���ADF�ա�DEC��SAS����
��CE��DF��![]() BD��
BD��
�뷨3��
֤�����ӳ�AB��F��ʹ��BF��BD������DF��CF����ͼ4��ʾ��

�ߡ�B��90������DF��![]() BD��
BD��
��Rt��ABD��Rt��CBF��
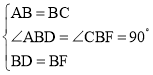 ��
��
���ABD�ա�CBF��SAS����
��AD��CF����BAD����BCF��
��AD��DE����DE��CF��
�ߡ�EDC����BAD�����EDC����BCF��
��DE��CF��
���ı���DFCEΪƽ���ı��Σ�
��CE��DF��![]() BD��
BD��

 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�