题目内容
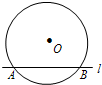
如图，PB，PC分别切⊙O于B、C两点，点A在⊙O上，若∠A=65°，则∠P=______．
在⊙O中，∠COB=2∠CAB-130°
∵PB、PC是⊙O的切线
所以∠PBO=∠PCO=90°
在四边形PBOC中，
∠P=360°-∠COB-∠PBO-∠PCO=50°，
所以答案为50°．
∵PB、PC是⊙O的切线
所以∠PBO=∠PCO=90°
在四边形PBOC中，
∠P=360°-∠COB-∠PBO-∠PCO=50°，
所以答案为50°．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
