题目内容
【题目】我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为 ![]() 的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将 ![]() 化为分数形式.
化为分数形式.
由于 ![]() ,
,
设 ![]()
则 ![]()
![]() 得
得 ![]() ,
,
解得 ![]() ,于是得
,于是得 ![]() .
.
同理可得 ![]() ,
,![]() .
.
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(![]() )
)![]() ,
,![]() ;
;
(![]() )将
)将 ![]() 化为分数形式,写出推导过程;
化为分数形式,写出推导过程;
(3)试比较 ![]() 与
与 ![]() 的大小:
的大小:![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”);
”);
【答案】(![]() )
)![]() ;
;![]() ;(
;(![]() )
) ![]() ;推导过程见解析;(3)
;推导过程见解析;(3) ![]() .
.
【解析】
(1)根据材料中的计算原理,分别列方程计算即可;
(2)根据材料中的计算原理,分别列方程计算即可;
(3)根据材料中的计算原理,分别列方程计算即可;
解:(![]() )由于
)由于 ![]() ,
,
设 ![]() ①
①
则 ![]() ②
②
②-①得 ![]() ,
,
解得 ![]() ,于是得
,于是得 ![]() ;
;
由于 ![]() ,
,
设 ![]() ①
①
则 ![]() ②
②
②-①得 ![]() ,
,
解得 ![]() ,于是得
,于是得 ![]() .
.
故答案为:![]() ;
;![]() ;
;
(![]() )
)![]()
设 ![]() ①
①
则 ![]() ②
②
②-① 得 ![]() ,解得
,解得 ![]() ,
,
![]() .
.
(3)由于 ![]() ,
,
设 ![]() ①
①
则 ![]() ②
②
②-①得 ![]() ,
,
解得 ![]() ,于是得
,于是得![]() =
=![]()
故答案为:=.

【题目】有这样一个问题:探究函数y=![]() 的图象与性质。小慧根据学习函数的经验,对函数y=
的图象与性质。小慧根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
(1)函数y=![]() 的自变量x的取值范围是__________;
的自变量x的取值范围是__________;
(2)列出y与x的几组对应值。请直接写出m的值,m=________;
x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
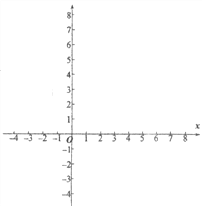
①_____________________________________________;
②____________________________________________。