题目内容
在Rt△ABC中,AB=3,BC=4,那么AC=________.
5或
分析:从当此直角三角形的两直角边分别是3和4时,当此直角三角形的一个直角边为3,斜边为4时这两种情况分析,再利用勾股定理即可求出第三边.
解答:(1)当AB、BC为直角边时,根据勾股定理得:
AC= =
= =5,
=5,
(2)当BC为斜边,AB为直角边时,根据勾股定理得:
AC=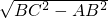 =
= =
= ,
,
当答案为:5或 .
.
点评:此题主要考查学生对勾股定理的理解和掌握,难度不大,是一道基础题.

分析:从当此直角三角形的两直角边分别是3和4时,当此直角三角形的一个直角边为3,斜边为4时这两种情况分析,再利用勾股定理即可求出第三边.
解答:(1)当AB、BC为直角边时,根据勾股定理得:
AC=
 =
= =5,
=5,(2)当BC为斜边,AB为直角边时,根据勾股定理得:
AC=
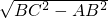 =
= =
= ,
,当答案为:5或
 .
.点评:此题主要考查学生对勾股定理的理解和掌握,难度不大,是一道基础题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径. 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )