题目内容
【题目】对于平面直角坐标系![]() 中的图形
中的图形![]() 和直线
和直线![]() ,给出如下定义:
,给出如下定义:![]() 为图形
为图形![]() 上任意一点,
上任意一点,![]() 为直线
为直线![]() 上任意一点,如果
上任意一点,如果![]() ,
,![]() 两点间的距离有最小值,那么称这个最小值为图形
两点间的距离有最小值,那么称这个最小值为图形![]() 和直线
和直线![]() 之间的“确定距离”,记作
之间的“确定距离”,记作![]() (
(![]() ,直线
,直线![]() ).
).
已知![]() ,
,![]() .
.
(1)求![]() (点
(点![]() ,直线
,直线![]() );
);
(2)![]() 的圆心为
的圆心为![]() ,半径为1,若
,半径为1,若![]() (
(![]() ,直线
,直线![]() )
)![]() ,直接写出
,直接写出![]() 的取值范围;
的取值范围;
(3)记函数![]() ,(
,(![]() ,
,![]() )的图象为图形
)的图象为图形![]() .若
.若![]() (
(![]() ,直线
,直线![]() )
)![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)![]() (点
(点![]() ,直线
,直线![]() );(2)
);(2)![]() 的值为
的值为![]() .(3)
.(3)![]() 的值为
的值为![]() 或
或![]() .
.
【解析】
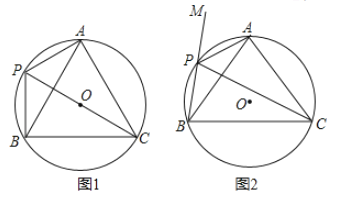
(1)如图1中,作OH⊥AB于H.求出OH即可解决问题.
(2)如图2中,作TH⊥AB于H,交⊙T于D.分两种情形求出d(⊙T,直线AB)=1时,点T的坐标即可.
(3)当直线经过点![]() 与直线AB平行时,此时两直线之间的距离为1,该直线的解析式为
与直线AB平行时,此时两直线之间的距离为1,该直线的解析式为![]() ,求出直线y=kx经过点E,点F时,k的值即可.
,求出直线y=kx经过点E,点F时,k的值即可.
解:(1)如图1中,作![]() 于
于![]() .
.

∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() (点
(点![]() ,直线
,直线![]() );
);
(2)如图2中,作![]() 于
于![]() ,交
,交![]() 于
于![]() .
.

当![]() (
(![]() ,直线
,直线![]() )
)![]() 时,
时,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
根据对称性可知,当![]() 在直线
在直线![]() 的右边,满足
的右边,满足![]() (
(![]() ,直线
,直线![]() )
)![]() 时,
时,![]() ,
,
∴满足条件的![]() 的值为
的值为![]() .
.
(3)如图3中,

当直线经过点![]() 与直线
与直线![]() 平行时,此时两直线之间的距离为1,该直线的解析式为
平行时,此时两直线之间的距离为1,该直线的解析式为![]() ,
,
当直线![]() 经过
经过![]() 时,
时,![]() ,
,
当直线![]() 经过
经过![]() ,
,![]() ,
,
综上所述,满足条件的![]() 的值为
的值为![]() 或
或![]() .
.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,DE 是⊙O的切线,连结OD,OE
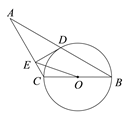
(1)求证:∠DEA=90°;
(2)若BC=4,写出求 △OEC的面积的思路.
【题目】如图,半圆O的直径AB=5cm,点M在AB上且AM=1cm,点P是半圆O上的动点,过点B作BQ⊥PM交PM(或PM的延长线)于点Q.设PM=xcm,BQ=ycm.(当点P与点A或点B重合时,y的值为0)小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:

(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 0 | 3.7 | ______ | 3.8 | 3.3 | 2.5 | ______ |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BQ与直径AB所夹的锐角为60°时,PM的长度约为______cm.
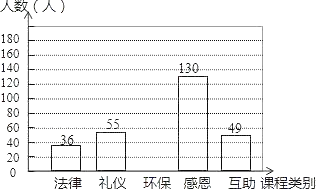
【题目】某校有学生3600人,在“文明我先行”的活动中,开设了“法律、礼仪、环保、感恩、互助”五门校本课程,规定每位学生必须且只能选一门,为了解学生的报名意向,学校随机调查了一些学生,并制成统计表和统计图:
课程类别 | 频数 | 频率 |
法律 | 36 | 0.09 |
礼仪 | 55 | 0.1375 |
环保 | m | a |
感恩 | 130 | 0.325 |
互助 | 49 | 0.1225 |
合计 | n | 1.00 |
(1)在这次调查活动中,学校采取的调查方式是 (填写“普查”或“抽样调查”)a= ,m= ,n= .
(2)请补全条形统计图,如果要画一个“校本课程报名意向扇形统计图”,那么“环保”类校本课程所对应的扇形圆心角应为 度;
(3)请估算该校3600名学生中选择“感恩”校本课程的学生约有多少人?