题目内容
阅读下面解题过程,然后解答问题:解方程:x4-x2-6=0
解:设y=x2,则原方程可化为y2-y-6=0,解得:y1=3,y2=-2
当y=3时,x2=3,?∴x=±
| 3 |
当y=-2时,x2=-2,原方程无实数根.
∴原方程的解为:x1=
| 3 |
| 3 |
这种解方程的方法叫“换元法”.
仔细体会这种方法的过程步骤,然后按照上述步骤解下列方程:
| x+1 |
| x |
| 2x |
| x+1 |
解:设y=
| x |
| x+1 |
解得:y1=
| ???? |
. |
| ???? |
. |
请你将后面的过程补充完整:
分析:设y=
,将y代入所求方程得
-2y=1,然后以y为未知数解方程可得y1,y2.
| x |
| x+1 |
| 1 |
| y |
解答:解:设y=
,将y代入原方程得,
-2y=1
两边同乘y得:1-2y2=y,
解之得:y=-1或y=
再将两解代入y=
得x有意义.
∴y1=-1,y2=
| x |
| x+1 |
| 1 |
| y |
两边同乘y得:1-2y2=y,
解之得:y=-1或y=
| 1 |
| 2 |
再将两解代入y=
| x |
| x+1 |
∴y1=-1,y2=
| 1 |
| 2 |
点评:考查换元法解方程,注意将所得的解代入原方程检验原方程是否有意义.

练习册系列答案
相关题目
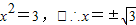 ;
;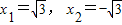
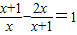
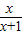 ,则原方程可化为关于y的方程:______
,则原方程可化为关于y的方程:______