题目内容
甲、乙两人进行射击比赛，7次射击命中的环数如下：
甲：6 7 9 8 7 10 9
乙：7 8 9 8 8 7 9
这两人7次射击命中环数的平均数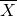
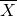甲=乙=8，则成绩比较稳定的是________．
乙
分析：根据方差公式S2=
[（x1-
）2+（x2-）2+…+（xn-）2]，计算出方差，根据方差的意义即可得到答案．
解答：S2甲=[（6-8）2+（7-8）2+（9-8）2+（8-8）2+（7-8）2+（10-8）2+（9-8）2]÷7=
，
S2乙=[（7-8）2+（8-8）2+（9-8）2+（8-8）2+（8-8）2+（7-8）2+（9-8）2]÷7=
，
∵
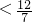
∴S2甲＞S2乙，
∴乙成绩比较稳定．
故答案为：乙．
点评：本题考查方差的定义与意义：一般地设n个数据，x1，x2，…xn的平均数为，则方差S2=[（x1-）2+（x2-）2+…+（xn-）2]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
分析：根据方差公式S2=
[（x1-）2+（x2-）2+…+（xn-）2]，计算出方差，根据方差的意义即可得到答案．解答：S2甲=[（6-8）2+（7-8）2+（9-8）2+（8-8）2+（7-8）2+（10-8）2+（9-8）2]÷7=
，S2乙=[（7-8）2+（8-8）2+（9-8）2+（8-8）2+（8-8）2+（7-8）2+（9-8）2]÷7=
，∵
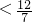
∴S2甲＞S2乙，
∴乙成绩比较稳定．
故答案为：乙．
点评：本题考查方差的定义与意义：一般地设n个数据，x1，x2，…xn的平均数为
，则方差S2=[（x1-）2+（x2-）2+…+（xn-）2]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立． 
练习册系列答案
轻松暑假总复习系列答案
相关题目
甲、乙两名学生进行射击练习，两人在相同条件下各射靶5次，射击成绩统计如下：
从射击成绩的平均数评价甲、乙两人的射击水平，则（ ）
| 命中环数（单位：环） | 7 | 8 | 9 | 10 |
| 甲命中相应环数的次数 | 2 | 2 | 0 | 1 |
| 乙命中相应环数的次数 | 1 | 3 | 1 | 0 |
| A、甲比乙高 | B、甲、乙一样 |
| C、乙比甲高 | D、不能确定 |
（2007•重庆）甲、乙两名学生进行射击练习，两人在相同条件下各射靶5次，射击成绩统计如下：
从射击成绩的平均数评价甲、乙两人的射击水平，则（ ）
A．甲比乙高
B．甲、乙一样
C．乙比甲高
D．不能确定
| 命中环数（单位：环） | 7 | 8 | 9 | 10 |
| 甲命中相应环数的次数 | 2 | 2 | 1 | |
| 乙命中相应环数的次数 | 1 | 3 | 1 |
A．甲比乙高
B．甲、乙一样
C．乙比甲高
D．不能确定
（2007•重庆）甲、乙两名学生进行射击练习，两人在相同条件下各射靶5次，射击成绩统计如下：
从射击成绩的平均数评价甲、乙两人的射击水平，则（ ）
A．甲比乙高
B．甲、乙一样
C．乙比甲高
D．不能确定
| 命中环数（单位：环） | 7 | 8 | 9 | 10 |
| 甲命中相应环数的次数 | 2 | 2 | 1 | |
| 乙命中相应环数的次数 | 1 | 3 | 1 |
A．甲比乙高
B．甲、乙一样
C．乙比甲高
D．不能确定
（2007•重庆）甲、乙两名学生进行射击练习，两人在相同条件下各射靶5次，射击成绩统计如下：
从射击成绩的平均数评价甲、乙两人的射击水平，则（ ）
A．甲比乙高
B．甲、乙一样
C．乙比甲高
D．不能确定
| 命中环数（单位：环） | 7 | 8 | 9 | 10 |
| 甲命中相应环数的次数 | 2 | 2 | 1 | |
| 乙命中相应环数的次数 | 1 | 3 | 1 |
A．甲比乙高
B．甲、乙一样
C．乙比甲高
D．不能确定