Question

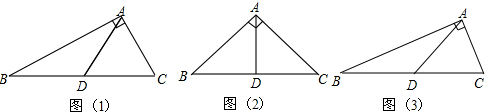
小聪同学为了探究“直角三角形斜边上的中线与斜边的数量关系”，他先画出了如图（1）和图（2）所示的两个特殊的直角三角形，其中∠BAC均为直角，AD均为斜边BC上的中线，图（1）中∠B=30°，图（2）中∠B=
45°．
（1）请猜想AD与BC之间的数量关系，并在图（1）和图（2）中选择一个加以证明．
（2）如图（3），在任意的Rt△ABC中，AD、BC之间的数量关系是否仍成立？请证明．

Answer 1

（1）猜想：AD=BC（或2AD=BC）．
理由：如图1，∵∠BAC=90°，∠B=30°，
∴BC=2AC．∠C=60°．
∵AD均为斜边BC上的中线，
∴BD=CD=BC=AC．
∴△ADC为等边三角形，
∴AD=CD=BC；

（2）答：AD=BC仍成立
证明：作EB⊥AB于B，延长AD交BE于点E，
∴∠ABE=90°．
∵∠BAC均为直角，
∴∠BAC=90°，
∴∠ABE+∠BAC=180°，
∴BE∥AC，
∴∠E=∠CAD，∠EBD=∠C．
在△EDB和△ADC中
，
∴△EDB≌△ADC（AAS），
∴BE=CA，AD=CD=AE．
在△ABE和△BAC中
，
∴△ABE≌△BAC（SAS），
∴AE=BC，
∴AD=BC．
分析：（1）如图1，由条件可以得出BC=2AC，就有CD=AC，由∠C═60°，就可以得出△ADC是等边三角形，就有AD=CD=BC而得出结论；
（2）作EB⊥AB于B，延长AD交BE于点E，可以得出△BDE≌△CDA，就可以得出BE=CA，AD=CD，进而可以得出△ABE≌△BAC就可以得出AE=BC，就可以得出结论．
点评：本题考查了直角三角形的性质的运用，平行线的性质的运用，全等三角形的判定及性质的运用，直角三角形斜边上的中线的性质的判定的运用，解答时证明三角形全等是关键．