Question

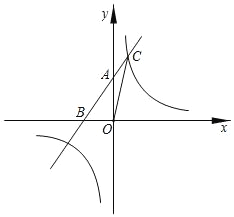
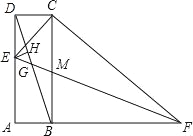
【题目】如图，一次函数y=(m+1)x+4的图像与x轴的负半轴相交于点A，与y轴相交于点B，且△OAB的面积为4.

（1）则= 及点的坐标为（ ）;

（2）过点B作直线BP与轴的正半轴相交于点P,且OP=4OA，求直线BP的解析式；

（3）将一次函数的图像绕点B顺时针旋转， 求旋转后的对应的函数表达式.

Answer 1

【答案】（1）1，（-2,0）；（2）；（3）

【解析】

（1）先求得OB=4，然后根据三角形面积求得OA的长，即可求得A的坐标，把A的坐标代入y=（m+1）x+4，即可求得m的值；

（2）利用OP=4OA=8可得到点P的坐标为（8，0），然后利用待定系数法求直线BP的函数解析式．

（3）直线绕点顺时针旋转 的直线交轴于点，过点 于点,作轴.根据容易证明，确定F点的坐标

解：（1）∵直线y=（m+1）x+4与y轴的交点B（0，4），∴OB=4，

∵S△OAB=4，

∴×OA×OB=4，

∴OA=2，∴A（-2，0），

把点A（-2，0）代入y=（m+1）x+4，得-2（m+1）+4=0，

解得m=1；

故答案为1，（-2,0）；

(2)，

设直线的解析式为，

将代入得，

直线的解析式为；

（ 3）直线绕点顺时针旋转 的直线交轴于点，过点 于点,作轴，

∵直线绕点顺时针旋转

∴∠ABE=,

∵,

∴∠BAF=

∴AF=AB, ∠BAO+∠FAE=

∵轴, ∠AOB=

∴∠FHA=∠AOB=, ∠ABO+∠BAO=

∴∠FAE=∠ABO

在中

∴

FH=OA=2, HA=OB=4

，

设直线的解析式为，

，

直线的解析式为.