Question

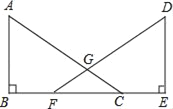
【题目】从边长为a的正方形中剪掉一个边长为b的正方形（如图），然后将剩余部分拼成一个长方形（如图）．

（1）上述操作能验证的等式是　 　；（请选择正确的一个）

A．a2－2ab＋b2＝(a－b)2 B．a2－b2＝(a＋b)(a－b） C．a2＋ab＝a(a＋b)

（2）应用你从（1）选出的等式，完成下列各题：

①已知x2－4y2＝12，x＋2y＝4，求x－2y的值．

②计算：（1－）（1－）（1－）…（1－）（1－）．

Answer 1

【答案】(1) B ;(2)① 3； ②.

【解析】

（1）观察图1与图2，根据两图形阴影部分面积相等，验证平方差公式即可；
（2）①已知第一个等式左边利用平方差公式化简，将第二个等式代入求出所求式子的值即可；②先利用平方差公式变形，再约分即可得到结果．

解：（1）根据图形得：a2-b2=（a+b）（a-b），
上述操作能验证的等式是B，
故答案为：B；

（2）①∵x2-4y2=（x+2y）（x-2y）=12，x+2y=4，
∴x-2y=12÷4=3；

②（1－）（1－）（1－）…（1－）（1－）

=（1－）（1+）（1－）（1+）…（1－）（1+）（1－）（1+）

=××××××…××××

=×

=.