题目内容
(1)如图1,AD为⊙O的直径,在圆上找一点B,将△AOB沿OB对折,和△COB能重合,连接CD,请问CD和BO有什么位置关系?并说明理由.(2)若B点移动到如图2的位置,则(1)问中的结论还成立吗?说明理由.
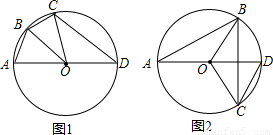
【答案】分析:(1)由折叠的性质可得∠BOA=∠BOC,再由圆周角定理可得∠CDA= ∠COA=∠BOA,从而可判断CD∥BO;
∠COA=∠BOA,从而可判断CD∥BO;
(2)结合(1)的思路,同样可得出结论.
解答:解:(1)由折叠的性质可得:∠BOA=∠BOC,
则可得∠BOA=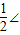 COA,
COA,
∵∠CDA= ∠COA(圆周角定理),
∠COA(圆周角定理),
∴∠BOA=∠CDA,
∴CD∥BO;
(2)由折叠的性质可得:∠ABO=∠CBO,
则可得∠BOD=∠OAB+∠OBA=2∠OBA,
∵∠CDO=2∠OBA(圆周角定理),
∴∠CDO=∠BOD,
∴CD∥BO;
点评:本题考查了翻折变换及圆周角定理的知识,注意掌握翻折变换的性质:翻折前后对应边相等、对应角相等.
 ∠COA=∠BOA,从而可判断CD∥BO;
∠COA=∠BOA,从而可判断CD∥BO;(2)结合(1)的思路,同样可得出结论.
解答:解:(1)由折叠的性质可得:∠BOA=∠BOC,
则可得∠BOA=
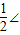 COA,
COA,∵∠CDA=
 ∠COA(圆周角定理),
∠COA(圆周角定理),∴∠BOA=∠CDA,
∴CD∥BO;
(2)由折叠的性质可得:∠ABO=∠CBO,
则可得∠BOD=∠OAB+∠OBA=2∠OBA,
∵∠CDO=2∠OBA(圆周角定理),
∴∠CDO=∠BOD,
∴CD∥BO;
点评:本题考查了翻折变换及圆周角定理的知识,注意掌握翻折变换的性质:翻折前后对应边相等、对应角相等.

练习册系列答案
相关题目

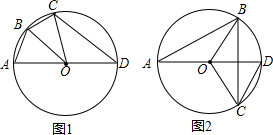 (1)如图1,AD为⊙O的直径,在圆上找一点B,将△AOB沿OB对折,和△COB能重合,连接CD,请问CD和BO有什么位置关系?并说明理由.
(1)如图1,AD为⊙O的直径,在圆上找一点B,将△AOB沿OB对折,和△COB能重合,连接CD,请问CD和BO有什么位置关系?并说明理由.
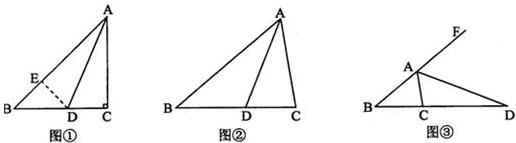
 如图,线段AD为△ABC中BC边上的中线.
如图,线段AD为△ABC中BC边上的中线.