题目内容
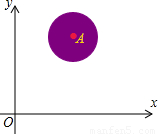
 如图,有一种Flash动画程序,屏幕上圆形区域表示红色小动物X,其中,A(3,3),⊙A的半径为1,用发射枪沿直线y=x+b发射子弹,当子弹遇到圆形区域X时,X就由红变黑.则b的取值范围为
如图,有一种Flash动画程序,屏幕上圆形区域表示红色小动物X,其中,A(3,3),⊙A的半径为1,用发射枪沿直线y=x+b发射子弹,当子弹遇到圆形区域X时,X就由红变黑.则b的取值范围为-
≤b≤
| 2 |
| 2 |
-
≤b≤
时,X能由红变黑.| 2 |
| 2 |
分析:解法(一):如图所示1,根据题意知,当直线y=x+b与⊙A有公共点时,X就由红变黑.所以,利用⊙A与直线y=x+b相切的性质、点到直线的距离公式来求b的取值范围即可.
解法(二):如图2所示,过圆心A作AD⊥BD于点D,过点O作OE⊥BD于点E,连接OA.易证四边形ADEO是矩形,AD=OE=1;然后在等腰直角△EOF中,利用勾股定理求得OF的长度.同理,求得OG的长度.
解法(二):如图2所示,过圆心A作AD⊥BD于点D,过点O作OE⊥BD于点E,连接OA.易证四边形ADEO是矩形,AD=OE=1;然后在等腰直角△EOF中,利用勾股定理求得OF的长度.同理,求得OG的长度.
解答: 解法(一):如图所示1,当直线y=x+b与⊙A相切时,且在⊙A的上方时,则过点A作AD⊥l1于点D,AD=1.
解法(一):如图所示1,当直线y=x+b与⊙A相切时,且在⊙A的上方时,则过点A作AD⊥l1于点D,AD=1.
∵A(3,3),x-y+b=0,
∴AD=
=1,即
=1,
解得,b=
,或b=-
(不合题意,舍去).
同理,当直线y=x+b与⊙A相切时,且在⊙A的下方时,b=-
.
则b的取值范围为-
≤b≤
;
故答案是:-
≤b≤
.
解法(二):如图2所示,过圆心A作AD⊥BD于点D,过点O作OE⊥BD于点E,连接OA.
则AD∥OE.
∵直线BD的解析式为y=x+b,
∴当x=0时,y=b.当y=0时,x=-b,
∴OB=OF=|b|,
∴∠OBF=∠OFB=45°.
又∵A(3,3),
∴∠FBO=∠AOC=45°,
∴BD∥OA,
∴四边形ADEO是矩形,
∴AD=OE.
根据题意知,直线BD与⊙A相切,则AD=OE=1.
在等腰Rt△EOF中,OE=1,∠EFO=45°,
∴OF=
OE=
.
同理求得OG=
,
∴b的取值范围是:-
≤b≤
;
故答案是:-
≤b≤
.
 解法(一):如图所示1,当直线y=x+b与⊙A相切时,且在⊙A的上方时,则过点A作AD⊥l1于点D,AD=1.
解法(一):如图所示1,当直线y=x+b与⊙A相切时,且在⊙A的上方时,则过点A作AD⊥l1于点D,AD=1.∵A(3,3),x-y+b=0,
∴AD=
| |1×3+(-1)×3+b| | ||
|
| |b| | ||
|
解得,b=
| 2 |
| 2 |
同理,当直线y=x+b与⊙A相切时,且在⊙A的下方时,b=-
| 2 |
则b的取值范围为-
| 2 |
| 2 |
故答案是:-
| 2 |
| 2 |
解法(二):如图2所示,过圆心A作AD⊥BD于点D,过点O作OE⊥BD于点E,连接OA.
则AD∥OE.
∵直线BD的解析式为y=x+b,
∴当x=0时,y=b.当y=0时,x=-b,

∴OB=OF=|b|,
∴∠OBF=∠OFB=45°.
又∵A(3,3),
∴∠FBO=∠AOC=45°,
∴BD∥OA,
∴四边形ADEO是矩形,
∴AD=OE.
根据题意知,直线BD与⊙A相切,则AD=OE=1.
在等腰Rt△EOF中,OE=1,∠EFO=45°,
∴OF=
| 2 |
| 2 |
同理求得OG=
| 2 |
∴b的取值范围是:-
| 2 |
| 2 |
故答案是:-
| 2 |
| 2 |
点评:本题考查了一次函数综合题、切线的性质.解答该题时,解法(一)中,利用了点到直线的距离公式d=
.解法(二)中利用了切线的性质、勾股定理等知识.
| |Ax0+By0+C| | ||
|

练习册系列答案
相关题目
 5、如图,有一种动画程序,屏幕上正方形区域ABCD表示黑色物体甲,其中,A (1,1),B (2,1),C (2,2),D (1,2),用信号枪沿直线y=2x+b发射信号,当信号遇到区域甲时,甲由黑变白.甲能由黑变白,则b的取值范围为( )
5、如图,有一种动画程序,屏幕上正方形区域ABCD表示黑色物体甲,其中,A (1,1),B (2,1),C (2,2),D (1,2),用信号枪沿直线y=2x+b发射信号,当信号遇到区域甲时,甲由黑变白.甲能由黑变白,则b的取值范围为( ) 12、如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线y=-2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为( )
12、如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线y=-2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为( ) 如图,有一种Flash动画程序,屏幕上圆形区域表示红色小动物X,其中,A(3,3),⊙A的半径为1,用发射枪沿直线y=x+b发射子弹,当子弹遇到圆形区域X时,X就由红变黑.则b的取值范围为________ 时,X能由红变黑.
如图,有一种Flash动画程序,屏幕上圆形区域表示红色小动物X,其中,A(3,3),⊙A的半径为1,用发射枪沿直线y=x+b发射子弹,当子弹遇到圆形区域X时,X就由红变黑.则b的取值范围为________ 时,X能由红变黑.