题目内容
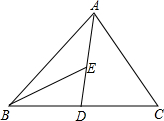 如图,AD为△ABC的中线,BE为三角形ABD中线,
如图,AD为△ABC的中线,BE为三角形ABD中线,(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)作△BED中BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?
分析:(1)利用三角形内角与外角的关系可直接得到答案;
(2)根据过直线外一点作已知直线的垂线的方法作图即可;
(3)根据中线的性质可得△BED的面积,再根据面积公式可得答案.
(2)根据过直线外一点作已知直线的垂线的方法作图即可;
(3)根据中线的性质可得△BED的面积,再根据面积公式可得答案.
解答: 解:(1)∵∠ABE=15°,∠BAD=40°,
解:(1)∵∠ABE=15°,∠BAD=40°,
∴∠BED=15°+40°=55°;
(2)如图所示:
(3)∵AD为△ABC的中线,
∴S△BAD=
S△ACB,
∵BE为三角形ABD中线,
∴S△BED=
S△BAD,
∵△ABC的面积为60,
∴S△BED=15,
∵BD=5,
∴EF=6.
 解:(1)∵∠ABE=15°,∠BAD=40°,
解:(1)∵∠ABE=15°,∠BAD=40°,∴∠BED=15°+40°=55°;
(2)如图所示:
(3)∵AD为△ABC的中线,
∴S△BAD=
| 1 |
| 2 |
∵BE为三角形ABD中线,
∴S△BED=
| 1 |
| 2 |
∵△ABC的面积为60,
∴S△BED=15,
∵BD=5,
∴EF=6.
点评:此题主要考查了三角形的中线,以及三角形的面积,三角形的内角与外角的关系,关键是掌握三角形的中线可以平分三角形的面积.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
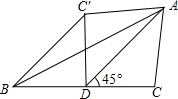 如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.
如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.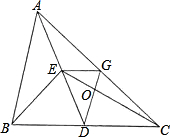 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线. 如图,AD为△ABC的中线,BE为三角形ABD中线,
如图,AD为△ABC的中线,BE为三角形ABD中线, 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线. 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.