题目内容
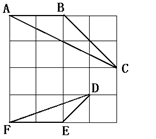
已知正方形纸片ABCD.如图1,将正方形纸片折叠,使顶点A落在边CD上的点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.

小题1:(1)请你找到一个与 相似的三角形,并证明你的结论;
相似的三角形,并证明你的结论;
小题2:(2)当AB=2,点P位于CD中点时,请借助图2画出折叠后的示意图,并求CG的长.

小题1:(1)请你找到一个与
 相似的三角形,并证明你的结论;
相似的三角形,并证明你的结论;小题2:(2)当AB=2,点P位于CD中点时,请借助图2画出折叠后的示意图,并求CG的长.
小题1:解:(1)与
 相似的三角形是
相似的三角形是 (或△FQG). ……… 1分
(或△FQG). ……… 1分 证明:∵四边形ABCD是正方形,
证明:∵四边形ABCD是正方形,∴∠A=∠B=∠C
 =∠D=90°. ……………………………… 2分
=∠D=90°. ……………………………… 2分由折叠知 ∠EPQ=∠A=90°.
∴∠1+∠3=90°,∠1+∠2=90°.
∴∠2=∠3. ……………………………………………………… 3分
∴
 ∽
∽
小题2:(2)正确画出示意图. …………………
 ……………………… 4分
……………………… 4分∵四边形ABCD是正方形,AB=2,
 ∴AB=BC=CD=DA=2.
∴AB=BC=CD=DA=2.设AE=x,则ED=2-x,EP= x.
∵P是CD的中点,
∴DP=PC=1.
在Rt△EDP中,∠D=90°,根据勾股定理,得
x2=(2-x)2+1.
解得x=
 .
.∴ED=
 .
. ………………………………………… 5分
………………………………………… 5分∵
 ∽
∽ ,
,∴
 .
.∴
 .
.∴ CG=
 .
. 略

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
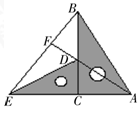
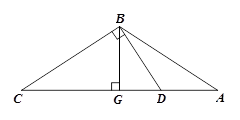
 S△ABC?
S△ABC?


 B.
B. 
 D.
D.