Question

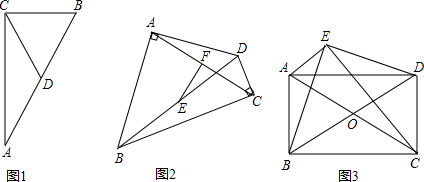
如图1，在矩形ABCD（AB＜BC）的BC边上取一点E，使BA=BE，作∠AEF=90°，交AD于F点，易证EA=EF．

（1）如图2，若EF与AD的延长线交于点F，证明：EA=EF仍然成立；
（2）如图3，若四边形ABCD是平行四边形（AB＜BC），在BC边上取一点E，使BA=BE，作∠AEF=∠ABE，交AD于F点．则EA=EF是否成立？若成立，请说明理由．
（3）由题干和（1）（2）你可以得出什么结论．

Answer 1

（1）证明：∵四边形ABCD是矩形，
∴∠B=90°，AD∥BC，
∵AB=BE，
∴∠AEB=∠FAE=45°，
∵∠AEF=90°，
∴∠FEC=180°-90°-45°=45°=∠AFE，
∴∠FAE=∠AFE，
∴EA=EF；

（2）解：EA=EF仍成立，
理由是：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠B+∠BAD=180°，
∵BA=BE，
∴∠AEB=∠BAE=∠FAE，
∵∠AEF=∠ABE，∠AEB+∠AEF+∠FEC=180°，
∴∠FEC=∠AFE，
∴EA=EF；

（3）解：在任意四边形ABCD中，只要满足AB＜BC，AD∥BC，在BC边上取一点E，使BA=BE，作∠AEF=∠ABE，交AD于F点，一定可得EA=EF．
分析：（1）根据矩形性质得出∠B=90°，AD∥BC，求出∠AEB=∠FAE=45°，求出∠FEC=∠AFE=45°，推出∠FAE=∠AFE，即可得出答案；
（2）根据平行四边形性质得出AD∥BC，推出∠B+∠BAD=180°，求出∠AEB=∠BAE=∠FAE，推出∠FEC=∠AFE，根据等腰三角形的判定推出即可；
（3）根据（1）（2）得出在任意四边形ABCD中，只要满足AB＜BC，AD∥BC，在BC边上取一点E，使BA=BE，作∠AEF=∠ABE，交AD于F点，一定可得EA=EF．
点评：本题考查了等腰三角形的判定，矩形的性质，平行四边形的性质，平行线的性质的应用，主要考查学生综合运用定理进行推理的能力．