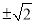题目内容
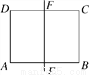
如图，某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度，他们通过调整测量位置，使斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上，已知DE＝0.5米，EF＝0.25米，目测点D到地面的距离DG＝1.5米，到旗杆的水平距离DC＝20米，求旗杆的高度．
阅读快车系列答案10袋大米的称重记录如下表所表示（单位：kg），求10袋大米的总质量.
每袋大米的质量（kg） | 47 | 50 | 46 | 51 |
袋数 | 3 | 2 | 1 | 4 |
小明的计算过程：10袋大米的总质量为47×3+50×2+46×1+51×4=······
（1）请你将小明的计算过程补充完整；
（2）若每袋大米的标准质量是50kg，请运用正负数的相关知识求这10袋大米的总质量；
（3）结合（2）中的计算说明，与10袋标准质量的大米相比，这10袋大米总计超过多少千克或不足多少千克？
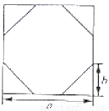
（1）见解析；（2）10袋大米的总质量是491kg；（3）比10袋标准质量的大米少9kg. 【解析】试题分析: （1）根据题中条件进行有理数的加减运算. （2）选择一个数作为基准,从而利用正负数表示一些数.本题中的基准数是50,这样就很容易用正负数记录10袋大米的质量, 然后用标准的10袋大米的总质量加上超出(或不足)的重量即可得到实际这10袋大米的总质量. （3）在(2)中的数...如图所示，在一个边长为a的正方形空地的四角上修建等腰直角三角形花坛，其直角边长均为b（2b<a），其余部分都种上草。
（1）请用含a，b的代数式表示草地部分的面积；
（2）若a=8m，b=3m，求该草地部分的面积.
阅读材料：若a-b>0，则a>b；若a-b=0，则a=b；若a-b<0，则a<b。运用此方法可进行有理数的大小比较，如比较5与3的大小。因为5-3=2>0，所以5>3，我们把这种比较大小的方法叫作“求差法”。
（1）请用“求差法”比较大小：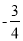 
与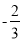
；
（2）请运用不同于（1）的方法比较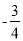
与
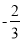的大小.
先简化、后求值：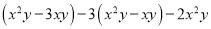 
，其中x=-2，y=-1.
（1）用代数式表示：a的3倍与b的差的一半；
（2）结合实际，说出代数式2a+3b的意义.
查看答案解方程：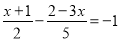 
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若x2﹣kxy+9y2是一个完全平方式，则k的值为（ ）
A. 3 B. ±6 C. 6 D. +3
B 【解析】∵x2?kxy+9y2是完全平方式， ∴?kxy=±2×3y?x， 解得k=±6. 故选：B.下列运算正确的是（ ）
A. 3x2+2x3=5x5 B. （π﹣3.14）0=0 C. 3﹣2=﹣6 D. （x3）2=x6
查看答案已知x≠1，(1＋x)(1－x)＝1－x2，(1－x)(1＋x＋x2)＝1－x3，(1－x)(1＋x＋x2＋x3)＝1－x4.
(1)根据以上式子计算：
①(1－2)×(1＋2＋22＋23＋24＋25)；
②2＋22＋23＋…＋2n(n为正整数)；
③(x－1)(x99＋x98＋x97＋…＋x2＋x＋1)．
(2)通过以上计算，请你进行下面的探索：
①(a－b)(a＋b)＝____________；
②(a－b)(a2＋ab＋b2)＝____________；
③(a－b)(a3＋a2b＋ab2＋b3)＝____________．
查看答案一项工程，甲、乙两公司合做，12天可以完成，共需付工费102000元；如果甲、乙两公司单独完成此项公程，乙公司所用时间是甲公司的1.5倍，乙公司每天的施工费比甲公司每天的施工费少1500元。
（1）甲、乙公司单独完成此项工程，各需多少天？
（2）若让一个公司单独完成这项工程，哪个公司施工费较少？
查看答案如图，点E，F在BC上，BE=CF，∠A=∠D，∠B=∠C，AF与DE交于点O．
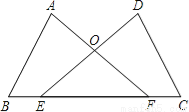
（1）求证：AB=DC；
（2）试判断△OEF的形状，并说明理由．
查看答案△ABC在平面直角坐标系中的位置如图所示．A（2，3），B（3，1），C（﹣2，﹣2）三点在格点上．
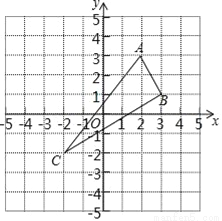
（1）作出△ABC关于y轴对称的△A1B1C1；
（2）直接写出△ABC关于x轴对称的△A2B2C2的各点坐标；
（3）求出△ABC的面积．
查看答案 试题属性- 题型：单选题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
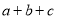就是完全对称式．下列三个代数式：
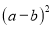；②
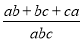；③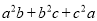
．其中是完全对称式的是（ ）．
B.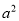 
的算术平方根是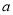
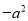一定没有平方根 D. 
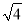的平方根是
