题目内容
设等边n边形的边长为a,面积为S,
(1)试探究等边三角形内部任一点P到三边的距离(d1+d2+d3)是否为定值?如果不是,请说明理由;如果是,请证明;
(2)请进一步探究等边四边形、等边五边形、…、等边n边形内任意一点到各边的距离之和是否为定值?对此,你能获得什么规律?
 解:(1)是定值.
解:(1)是定值.证明:如图,△ABC是等边三角形,点P是等边三角形内部任一点.
S△APB=
 a•PE,S△CPB=
a•PE,S△CPB= a•PF,S△APC=
a•PF,S△APC= a•PG,
a•PG,于是S△APB+S△CPB+S△APC=
 a•PE+
a•PE+ a•PF+
a•PF+ a•PG,
a•PG,即
 a•PE+
a•PE+ a•PF+
a•PF+ a•PG=S,
a•PG=S,PE+PF+PG=
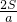 ,为定值.
,为定值.即d1+d2+d3=
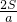 ,为定值.
,为定值.(2)同(1)中证法,等边四边形、等边五边形、…、等边n边形内任意一点到各边的距离之和均为定值,规律为d1+d2+d3+…+dn=
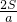 .
.分析:(1)将大正三角形化为小三角形,根据三角形面积公式解答;
(2)将正多边形化为小三角形,根据三角形面积公式解答.
点评:此题但难度不大,只要想到用面积法便可迎刃而解.

练习册系列答案
相关题目

