题目内容
将x3-ax2-2ax+a2-1分解因式得 ________.
[a-(x-1)][a-(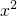 +x+1)]
+x+1)]
分析:代数式x3-ax2-2ax+a2-1,若视x为主元,则为三次四项式,而视a为主元,则为二次三项式,故可视a为主元;因为(x-1)×(x2+x+1)=x3-1,(x-1)+(x2+x+1)=x2+2x,所以利用十字相乘法分解因式即可.
解答:把a看做主元,变形得,
原式=a2-ax2-2ax+x3-1,
=a2-(x2+2x)a+(x-1)×(x2+x+1),
=[a-(x-1)][a-(x2+x+1)].
故答案为:[a-(x-1)][a-(x2+x+1)].
点评:本题考查十字相乘法分解因式,运用十字相乘法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程;本题解答的关键是找到主元.
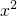 +x+1)]
+x+1)]分析:代数式x3-ax2-2ax+a2-1,若视x为主元,则为三次四项式,而视a为主元,则为二次三项式,故可视a为主元;因为(x-1)×(x2+x+1)=x3-1,(x-1)+(x2+x+1)=x2+2x,所以利用十字相乘法分解因式即可.
解答:把a看做主元,变形得,
原式=a2-ax2-2ax+x3-1,
=a2-(x2+2x)a+(x-1)×(x2+x+1),
=[a-(x-1)][a-(x2+x+1)].
故答案为:[a-(x-1)][a-(x2+x+1)].
点评:本题考查十字相乘法分解因式,运用十字相乘法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程;本题解答的关键是找到主元.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目