Question

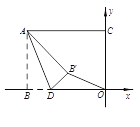
【题目】如图，矩形ABOC中，A点的坐标为（－4，3），点D是BO边上一点，连接AD，把△ABD沿AD折叠，使点B落在点B′处．当△ODB′为直角三角形时，点D的坐标为___________．

Answer 1

【答案】，

【解析】

首先利用勾股定理求出AO，再分两种情形：①如图1，当∠DB′O=90°时．②如图2，当∠B′DO=90，分别求解即可

分两种情况讨论：（1）点B′在边AC上时，∠ODB′＝90°，此时BD=DB′=AB=3，所以OD=1，所以点D的坐标为（-1,0）；（2）点B′在对角线AO上时，∠DB′O＝90°，由折叠可得：AB=AB′=3，因为OB=4，所以由勾股定理可得：OA=5，所以OB′＝5-3=2，设OD=x，则BD=DB′=4-x，在Rt△ODB′中，由勾股定理可得：,所以，解得x=，所以点D的坐标为（-,0）；所以点D的坐标为，或．