题目内容
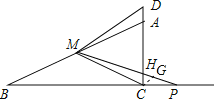
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点M是AB的中点,连接MC,点P是线段BC延长线上一点,且
,点M是AB的中点,连接MC,点P是线段BC延长线上一点,且![]() ,连接MP交AC于点H.将射线MP绕点M逆时针旋转
,连接MP交AC于点H.将射线MP绕点M逆时针旋转![]() 交线段CA的延长线于点D.
交线段CA的延长线于点D.
(1)找出与![]() 相等的角,并说明理由.
相等的角,并说明理由.
(2)如图2,![]() ,求
,求![]() 的值.
的值.
(3)在(2)的条件下,若![]() ,求线段AB的长.
,求线段AB的长.

【答案】(1)![]() ;理由见解析;(2)
;理由见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)![]() .由直角三角形的性质和旋转的性质推知即可;
.由直角三角形的性质和旋转的性质推知即可;
(2)如图,过点C作![]() 交MP于点G.构造全等三角形(
交MP于点G.构造全等三角形(![]() )和相似三角形(
)和相似三角形(![]() ),根据相似三角形的对应边成比例求得
),根据相似三角形的对应边成比例求得![]() 的值.
的值.
(3)由(2)中相似三角形的性质和等量代换推知![]() .故
.故![]() .易得
.易得![]() .由(2)知,
.由(2)知,![]() ,则
,则![]() .故
.故![]() ,
,![]() .根据题意得到:
.根据题意得到:![]() ,所以该相似三角形的对应边成比例:
,所以该相似三角形的对应边成比例:![]() .将相关线段的长度代入求t的值,所以
.将相关线段的长度代入求t的值,所以![]() .
.
(1)![]() .
.
理由如下:∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
由旋转的性质知,![]() .
.
∴![]() ;
;
(2)如图,过点C作![]() 交MP于点G.
交MP于点G.
∴![]() ,
,![]() .
.
∵![]() ,点M是AB的中点,
,点M是AB的中点,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 与
与![]() 中,
中,
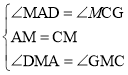
∴![]() .
.
∴![]() .
.
∵![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
∴![]() .
.
∴![]() ;
;
(3)如图,由(2)知![]() .则
.则![]() .
.
∵![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
由(2)知,![]() ,则
,则![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() ,即
,即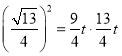 .
.
解得![]() ,
,![]() (舍去).
(舍去).
∴![]() .
.

练习册系列答案
相关题目