题目内容
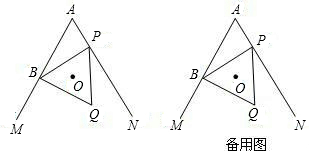
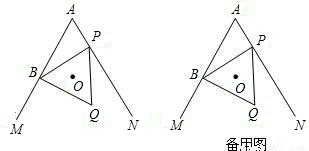
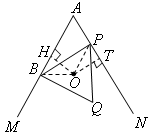
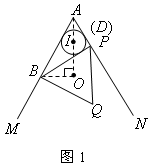
已知:∠MAN=60°,点B在射线AM上,AB=4(如图),P为直线AN上一动点,以BP为边作等边三角形BPQ(点B,P,Q按顺时针排列),O是△BPQ的外心。

(1)当点P在射线AN上运动时,求证:点O在∠MAN的平分线上;
(2)当点P在射线AN上运动(点P与点A不重合)时,AO与BP交于点C,设AP=x,AC·AO=y,求y关于x的函数解析式,并写出函数的定义域;
(3)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离。
(2)当点P在射线AN上运动(点P与点A不重合)时,AO与BP交于点C,设AP=x,AC·AO=y,求y关于x的函数解析式,并写出函数的定义域;
(3)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离。
| 解:(1)证明:如图: 连结OB,OP, ∵O是等边三角形BPQ的外心, ∴OB=OP, 圆心角 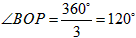 , ,当OB不垂直于AM时,作OH⊥AM,OT⊥AN,垂足分别为H,T, 由 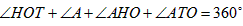 ,且∠A=60°, ,且∠A=60°, , ,∴ 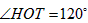 , ,∴  , ,∴  , ,∴OH=OT, ∴点O在∠MAN的平分线上 当  时, 时, , ,即OP⊥AN, ∴点O在∠MAN的平分线上, 综上所述,当点P在射线AN上运动时,点O在∠MAN的平分线上; |
 |
| (2)如图: ∵AO平分∠MAN,且∠MAN=60°, ∴  , ,由(1)知,OB=OP,∠BOP=120°, ∴ 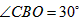 , ,∴ 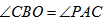 , ,∴  , ,∴  , ,∴ 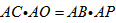 , ,∴y=4x, 定义域为x>0; |
 |
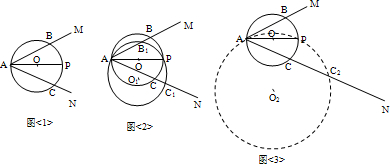
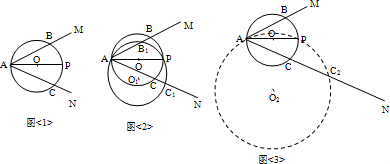
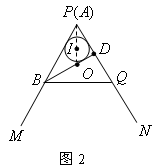
(3)①如图1:当BP与圆I相切时,AO=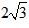 , ,②如图2,当BP与圆I相切时,AO= 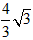 ; ;③如图3,当BQ与圆I相切时,AO=0。 |
   |

练习册系列答案
相关题目