题目内容
已知:抛物线 与x轴的两个交点分别为A(1,0)和B(3,0),与y轴交于点C.
与x轴的两个交点分别为A(1,0)和B(3,0),与y轴交于点C.
(1)求此二次函数的解析式;
(2)写出点C的坐标________,顶点D的坐标为__________;
(3)将直线CD沿y轴向下平移3个单位长度,求平移后直线m的解析式;
(4)在直线m上是否存在一点E,使得以点E、A、B、C为顶点的四边形是梯形,如果存在,请直接写出所有满足条件的E点的坐标__________________________________(不必写出过程).
(2)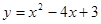 ;(2)(0,3),(2,-1);(3)
;(2)(0,3),(2,-1);(3)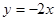 ;(4)(-1,2)或(-1.5,3)
;(4)(-1,2)或(-1.5,3)
解析试题分析:(1)由抛物线 过点A(1,0)和B(3,0)根据待定系数法列方程组求解即可;
过点A(1,0)和B(3,0)根据待定系数法列方程组求解即可;
(2)根据(1)中求得的函数解析式结合二次函数的性质求解即可;
(3)先设CD: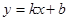 ,由点C、D的坐标根据待定系数法即可求得直线CD的解析式,再根据直线的平移规律:上加下减,即可求得结果;
,由点C、D的坐标根据待定系数法即可求得直线CD的解析式,再根据直线的平移规律:上加下减,即可求得结果;
(4)根据梯形的对边平行再结合一次函数的性质求解即可.
试题解析:(1)∵抛物线 过点A(1,0)和B(3,0)
过点A(1,0)和B(3,0)
∴ ,解得
,解得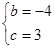
∴此二次函数的解析式为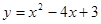 ;
;
(2)在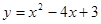 中,当x=0时,y=3,所以点C的坐标为(0,3)
中,当x=0时,y=3,所以点C的坐标为(0,3)
因为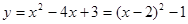 ,所以顶点D的坐标为(2,-1);
,所以顶点D的坐标为(2,-1);
(3)设CD: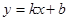
∵图象过点(0,3),(2,-1)
∴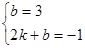 ,解得
,解得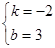
∴CD: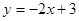 ,沿y轴向下平移3个单位长度后直线m的解析式为
,沿y轴向下平移3个单位长度后直线m的解析式为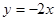 ;
;
(4)(-1,2)或(-1.5,3).
考点:二次函数的综合题

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
某商品的进价为每千克40元,销售单价与月销售量的关系如下表(每千克售价不能高于65元):
| 销售单价(元) | 50 | 53 | 56 | 59 | 62 | 65 |
| 月销售量(千克) | 420 | 360 | 300 | 240 | 180 | 120 |
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每千克商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?



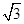 )为圆心,以2为半径的圆与
)为圆心,以2为半径的圆与 轴交于A、B两点.
轴交于A、B两点.
 的图象经过点A、B,试确定此二次函数的解析式.
的图象经过点A、B,试确定此二次函数的解析式. 经过(0,-1),(3,2)两点.求它的解析式及顶点坐标.
经过(0,-1),(3,2)两点.求它的解析式及顶点坐标.
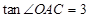 ,求抛物线的表达式;
,求抛物线的表达式;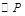 相离、相切、相交.
相离、相切、相交.