题目内容
已知:△ABC中,AD为中线,∠BAD=60°,AB=10,BC=4 ,求AC的长.
,求AC的长.
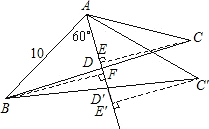 解:分别过B、C作BF⊥AD于F,CE⊥AD于E,
解:分别过B、C作BF⊥AD于F,CE⊥AD于E,在Rt△AFB中,∠BAF=60°,AB=10,
sin∠BAF=
 ,
,∴BF=ABsin∠BAF=5
 .
.cos∠BAF=
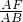 ,
,∴AF=ABcos∠BAF=5.
BC=4
 ,AD为中线,
,AD为中线,∴BD=DC=2
 .
.在Rt△BFD中,DF=
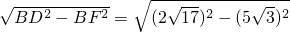 =1,
=1,∵D为BC中点,∴BD=CD,
又CE⊥AD,BF⊥AD,
∴∠ADC=∠BDF.
∴△BDF≌△CDE(AAS).
∴DE=DF=1.
∴AE=5-2=3,CE=BF=5
 .
.在Rt△AEC中,AC=
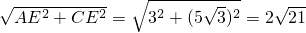 ,
,又若△ABC'时,AE'=5+2=7,C'E'=5
 ,
,在Rt△AE'C'中,A'C'=
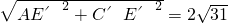 ,
,∴AC的长为2
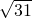 或
或 .
.分析:由条件知,AC的位置分两种情况,一种为从点向AD作的垂线不三角形的内部,另一种是该线在三角形的外部,因而分别利用锐角三角函数的概念,勾股定理,全等三角形的性质来计算.
点评:考查综合应用解直角三角形、直角三角形性质,全等三角形的判定和性质,也考查逻辑推理能力和运算能力.注意要分类讨论.

练习册系列答案
相关题目
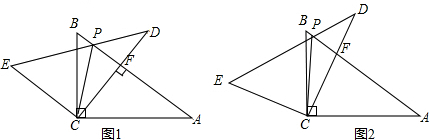
 如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示)
如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示) 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.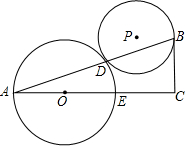 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,