题目内容
如图，在平行四边开ABCD中，过点A作AE⊥BC，垂足为E，连接DE，且∠AFE=∠B。
（1）求证：ΔADF∽ΔDEC
（2）
 |
（1）证明：∵四边形ABCD是平行四边形
∴∠B+∠C=1800
又∵∠AFE+∠AFD=1800 ∠AFE=∠B
∴∠C=∠AFD
而AD∥BC
∴∠DEC=∠ADF
∴ΔADF∽ΔDEC
（2）∵ΔADF∽ΔDEC
∴
∴ DE=12
又∵∠B+∠BAE+∠EAD=1800 ∠B+∠BAE=90
∴∠EAD=900
在RtΔDAE中
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
－
＝0 
先化简，再求值， 
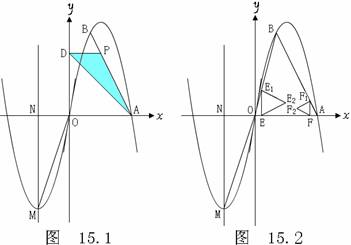②过线段OA上的两点E、F分别作x轴的垂线，交折线 O –B -A于点E1、F1，再分别以线段EE1、FF1为边作如图15.2所示的等边△EE1E2、等边△FF1F2,点E以每秒1个单位长度的速度从点O向点A运动，点F以每秒1个单位长度的速度从点A向点O运动，当△EE1E2有一边与△FF1F2的某一边在同一直线上时，求时间t的值.