Question

（本小题满分14分）
如图所示，抛物线经过原点，与轴交于另一点,直线与两坐标轴分别交于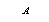、两点，与抛物线交于、两点.

【小题1】（1）求直线与抛物线的解析式；
【小题2】（2）若抛物线在轴上方的部分有一动点，
求的面积最大值；
【小题3】（3）若动点保持（2）中的运动路线，问是否存在点
，使得的面积等于面积的？若存在，请求出点的坐标；
若不存在，请说明理由．

Answer 1

【小题1】解：（1）把点B、C的坐标代入
   解方程组得
 直线的解析式是…………（2分）
把点O、B、C的坐标代入
                  解方程组得 
 抛物线的解析式是…………（4分）
【小题2】（2） 配方得
 顶点坐标是…………（5分）
当y = 0时，    点N（，0）…………（6分）
当P点运动到顶点的位置时，的面积最大，最大值是：
…………（8分）
【小题3】（3）不存在…………（9分）
直线与x轴的交点D（4,0），与y轴交点A（0,4）
，   
∴，
∴        ∴…………（11分）
∵点P在上，且位于轴的上方，
∴  代入
得到，即，
∴，它们与矛盾               
∴点P不存在
即在抛物线上不存在点P，使得的面积等于面积的

解析