Question

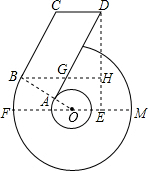
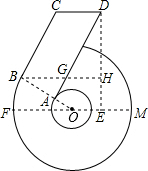
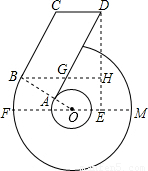
 已知“6”字形图中，FM是大⊙O的直径， BC与大⊙O相切于B, OB与小⊙O相交于A, AD∥BC，CD∥BH∥FM, DH⊥BH于H，设∠FOB＝30°，OB=4, BC=6.

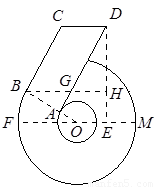
   ﹙1﹚求证:AD为小⊙O的切线;

﹙2﹚求DH的长.﹙结果保留根号﹚

 

Answer 1

【答案】

（1）证明见解析(2)

【解析】（1）证明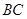：∵是大⊙O的切线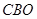，∴∠＝90°.

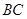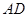              ∵∥,  ∴∠BAD＝90°.即⊥.

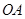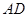          又∵点A在小⊙O上，∴AD是小⊙O的切线. ············· 2分

 (2)∵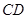∥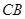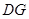，∥,∴四边形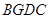是平行四边形.

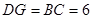    ∴.      ························· 3分

  ∵∥，∴.

∴.

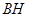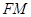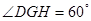又∵,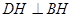

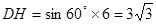∴.   5分

（1）证OA⊥AD即可．由BC与大⊙O相切于B，得OB⊥BC；AD∥BC，则OB⊥AD．得证．

（2）易证四边形BCDG是平行四边形，则DG=BC=6；由∠FOB=30°，BH∥FM可得∠OBG=30°，∠BGA=60°=∠DGH．在Rt△DGH中运用三角函数求解．