Question

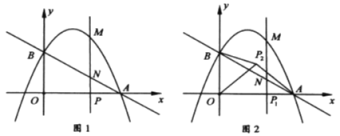
【题目】如图1，抛物线与轴交于点，与轴交于点，在轴上有一动点，过点作轴的垂线交直线于点，交抛物线于点.

(1)求的值;

(2)若，求的值，

(3)如图2，在(2)的条件下，设动点对应的位置是，将线段绕点逆时针旋转得到，旋转角为，连接、，求的最小值.

Answer 1

【答案】（1 a= ；（2）m=3；（3）AP2+BP2的最小值为 ．

【解析】

（1）把A点坐标代入可得到关于a的方程，可求得a的值；
（2）由△OAB∽△PAN可用m表示出PN，且可表示出PM，由条件可得到关于m的方程，则可求得m的值；
（3）在y轴上取一点Q，使 ，可证得△P2OB∽△QOP2，则可求得Q点坐标，则可把AP2+BP2化为AP2+QP2，利用三角形三边关系可知当A、P2、Q三点在一条线上时有最小值，则可求得答案．

解：（1）∵A（4，0）在抛物线上，
∴0=16a+4（a+2）+2，解得a= ；
（2）由（1）可知抛物线解析式为y=x2+x+2，令x=0可得y=2，
∴OB=2，
∵OP=m，
∴AP=4-m，
∵PM⊥x轴，
∴△OAB∽△PAN，
∴，即 ，
∴PN=（4-m），
∵M在抛物线上，
∴PM=m2+m+2，
∵PN：MN=1：3，
∴PN：PM=1：4，
∴m2+m+2=4×（4-m），
解得m=3或m=4（舍去）；
（3）在y轴上取一点Q，使 ，如图，

由（2）可知P1（3，0），且OB=2，
∴ ，且∠P2OB=∠QOP2，
∴△P2OB∽△QOP2，
∴ ，
∴当Q（0， ）时QP2=BP2，
∴AP2+BP2=AP2+QP2≥AQ，
∴当A、P2、Q三点在一条线上时，AP2+QP2有最小值，
∵A（4，0），Q（0，），
∴AQ= ，即AP2+BP2的最小值为 ．

故答案为：（1 a= ；（2）m=3；（3）AP2+BP2的最小值为 ．