��Ŀ����
����Ŀ������̽��
������ͼ�ΰ���ij�ַ�������任����һ�ּ���ͼ�εĹ��̽������α任����ת�任�Ǽ��α任��һ�ֻ���ģ�ͣ�������ת��������ʹͼ�εļ��������������֣�����ͽ����е�Ԫ���ɷ�ɢ��Ϊ���У��֮��Ĺ�ϵ������ˣ��Ӷ�������������ת����
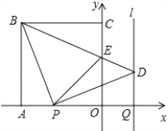
�����������ͼ1��![]() �DZ߳�Ϊ1�ĵȱ������Σ�
�DZ߳�Ϊ1�ĵȱ������Σ�![]() Ϊ
Ϊ![]() �ڲ�һ�㣬����
�ڲ�һ�㣬����![]() ����
����![]() ����Сֵ��
����Сֵ��
����ͨ��ת����������������һ�㷢���������߶�(������)ת��Ϊ������֮�������(����Ϊ��)��������������֮���߶����������Сֵ(����Ϊֱ)��
����������ͼ2����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ��
��![]() ������
������![]() ��
��![]() ����
����![]() ��
��![]() ���ڵ�
���ڵ�![]() ����֪
����֪![]() ��
��![]() ����
����![]() ��
��![]() ����֪
����֪![]() Ϊ�������Σ���
����������![]() ��
��
��![]() ����ˣ���
����ˣ���![]() ����ʱ��
����ʱ��![]() ����Сֵ��
����Сֵ��![]() ��
��
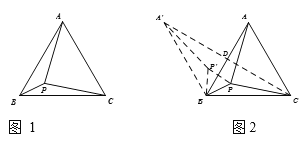
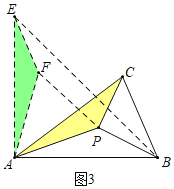
ѧ�����ã�(1)��ͼ3����![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �ڲ�һ�㣬����
�ڲ�һ�㣬����![]() ��
��![]() ����
����![]() ����Сֵ��__________��
����Сֵ��__________��
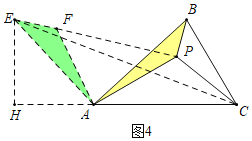
(2)��ͼ4����![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �ڲ�һ�㣬����
�ڲ�һ�㣬����![]() ��
��![]() ����
����![]() ����Сֵ��
����Сֵ��
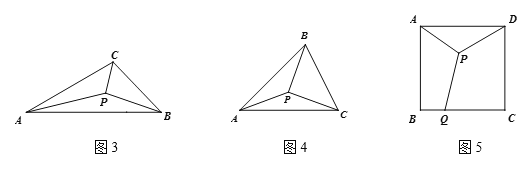
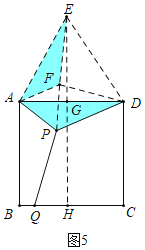
(3)��ͼ5��![]() �DZ߳�Ϊ2��������
�DZ߳�Ϊ2��������![]() ��һ�㣬
��һ�㣬![]() Ϊ��
Ϊ��![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ����
����![]() ����Сֵ��
����Сֵ��
���𰸡���1��5����2��![]() ����3��
����3��![]() .
.
��������
��1����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ����֪
����֪![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ��ת��Ϊ������֮������ߣ�����Ϊ�ۣ��������á�����֮���߶���̡�����Сֵ������Ϊֱ����
��ת��Ϊ������֮������ߣ�����Ϊ�ۣ��������á�����֮���߶���̡�����Сֵ������Ϊֱ����
��2����![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ����֪
����֪![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ����
����![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ��ת��Ϊ������֮������ߣ�����Ϊ�ۣ��������á�����֮���߶���̡�����Сֵ������Ϊֱ����
��ת��Ϊ������֮������ߣ�����Ϊ�ۣ��������á�����֮���߶���̡�����Сֵ������Ϊֱ����
��3����ͼ5�У���![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ������֪
������֪![]() �ǵȱ������Σ�ת��Ϊ������֮������ߣ�����Ϊ�ۣ��������á����߶���̡�����Сֵ��
�ǵȱ������Σ�ת��Ϊ������֮������ߣ�����Ϊ�ۣ��������á����߶���̡�����Сֵ��
�⣺��1����ͼ3�У�
��![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ��
��
��![]() ��
��![]() ����CAE=PAF=60����
����CAE=PAF=60����
��AE=AC=3��AF=AP��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
�ߡ�BAC=30�㣬
��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ����СֵΪ5��
����СֵΪ5��
�ʴ�Ϊ5��
��2����ͼ4�У�
��![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ��
��
��AF=AP����FAP=90�㣬
��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
��FP=![]() ��
��
�ߡ�BAC=45�㣬
��![]() ��
��![]() ��
��
��![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ��
��
��![]() ��
�У�
![]() ��
��![]() ��
��![]()
![]() ��
��
��![]() ��
�У�![]()
![]()
![]() ��
��
![]() ��
��
![]() ����СֵΪ
����СֵΪ![]() ��
��
��3����ͼ5�У���![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]() ������֪
������֪![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
![]() ��
��
��֪![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ����СֵΪ
����СֵΪ![]() ��
��

 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д�