Question

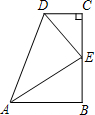如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，AB=6cm，DC=2cm，求AD的长．（提示：过点E作EF⊥AD，垂足为F）

Answer 1

分析：过点E作EF⊥AD，垂足为F，根据角平分线上的点到角的两边的距离相等可得EC=EF，再求出EB=EF，然后分别利用“HL”证明△CDE和△FDE全等，△ABE和△AFE全等，根据全等三角形对应边相等可得AB=AF，CD=DF，从而得到AD=AB+CD．

解答：解：如图，过点E作EF⊥AD，垂足为F，
∵DE平分∠ADC，∠C=90°，
∴EC=EF，
∵E是BC的中点，
∴EC=EB，
∴EB=EF，
在△CDE和△FDE中，

DE=DE EC=EF

，
∴△CDE≌△FDE（HL），
∴CD=DF，
在△ABE和△AFE中，

AE=AE EB=EF

，
∴△ABE≌△AFE（HL），
∴AB=AF，
∵AD=AF+DF，
∴AD=AB+CD=6+2=8cm．

点评：本题考查了角平分线上的点到角的两边的距离相等的性质，全等三角形的判定与性质，作辅助线构造出全等三角形是解题的关键，也是本题的难点．