题目内容
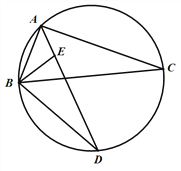
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.

【答案】(1)证明见解析;(2)PQ的长是![]() .
.
【解析】试题分析:⑴先根据线段垂直平分线的性质证明QB=QE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形ABGE是平行四边形,再根据菱形的判定即可得出结论.
⑵根据三角形中位线的性质可得![]() ,设
,设![]() ,则
,则
![]() ,在Rt△ABE中,根据勾股定理可得
,在Rt△ABE中,根据勾股定理可得![]() ,解得BE=10,
,解得BE=10,
得到![]() ,设
,设![]() ,则
,则![]() ,
, ![]() ,计算得出
,计算得出![]() ,在Rt△BOP中,根据勾股定理可得
,在Rt△BOP中,根据勾股定理可得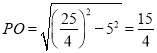 ,由
,由![]() 即可求解.
即可求解.
试题解析:
(1)证明:∵ PQ垂直平分BE,
∴ QB=QE,OB=OE,
∵ 四边形ABCD是矩形,
∴ AD∥BC,
∴ ∠ PEO=∠ QBO,
在△ BOQ与△ EOP中,
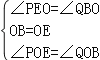 ,
,
∴ △ BOQ≌ △ EOP(ASA),
∴ PE=QB,
又∵ AD∥BC,
∴ 四边形BPEQ是平行四边形,
又∵ QB=QE,
∴ 四边形BPEQ是菱形;
(2)解:∵ O,F分别为PQ,AB的中点,
∴ AE+BE=2OF+2OB=18,
设AE=x,则BE=18﹣x,
在Rt△ ABE中,62+x2=(18﹣x)2,
解得x=8,
BE=18﹣x=10,
∴ OB=![]() BE=5,
BE=5,
设PE=y,则AP=8﹣y,BP=PE=y,
在Rt△ ABP中,62+(8﹣y)2=y2,解得y=![]() ,
,
在Rt△ BOP中,PO=![]() =
=![]() ,
,
∴ PQ=2PO=![]() .
.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目