题目内容
已知如图,AB=AC, ∠BAC=90 °,AE 是过A 点的一条直线, 且B 、C 在DE 的异侧,BD ⊥AE 于D,CE ⊥AE 于E, 求证:BD=DE+CE
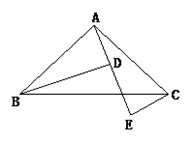
解：∵BD ⊥AE 于D,CE ⊥AE 于E
∴∠ADB= ∠AEC=90 °
∵∠BAC=90 °
∴∠ABD+ ∠BAD= ∠CAE+ ∠BAD
∴∠ABD= ∠CAE 在△ABD 和△CAE 中
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE
∵AE=AD+DE
∴BD=CE+DE
∴∠ADB= ∠AEC=90 °
∵∠BAC=90 °
∴∠ABD+ ∠BAD= ∠CAE+ ∠BAD
∴∠ABD= ∠CAE 在△ABD 和△CAE 中
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE
∵AE=AD+DE
∴BD=CE+DE
练习册系列答案
相关题目
已知如图，AC=5，AB=3，边BC上的中线AD=2，求△ABC的面积．
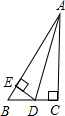已知如图，AC⊥BC，DE⊥AB，AD平分∠BAC，下面结论错误的是（ ）| A、BD+ED=BC | B、DE平分∠ADB | C、AD平分∠EDC | D、ED+AC＞AD |
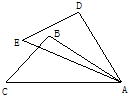15、已知如图，AC=AE，AB=AD，∠CAE=∠BAD．求证：BC=DE．