题目内容
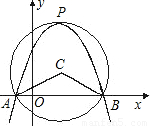
(2010•泉港区质检)如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点.(1)求出A,B两点的坐标;
(2)若有一条开口向下的抛物线经过点A,B,且其顶点P在⊙C上,请求出此抛物线的解析式.
【答案】分析:(1)过C作AB的垂线,设垂足为H,在Rt△CAH中,已知圆的半径和CH的长(由C点坐标获得),利用勾股定理即可求得AH的长,进而可得到点A的坐标,B点坐标的求法相同.
(2)根据抛物线和圆的对称性知:C、P都在弦AB的垂直平分线上,已知了C点坐标和圆的半径,即可得到点P的坐标,而P为抛物线顶点,可将所求抛物线设为顶点坐标式,然后将A点坐标代入抛物线的解析式中,即可求得待定系数的值,从而求出该抛物线的解析式.
解答: 解:(1)过点C作CH⊥x轴,H为垂足;
解:(1)过点C作CH⊥x轴,H为垂足;
又∵C(1,1),
∴CH=OH=1;(1分)
∴在Rt△CHB中, ;(3分)
;(3分)
∵CH⊥AB,CA=CB,
∴AH=BH;
故A(1-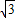 ,0),B(1+
,0),B(1+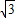 ,0).(5分)
,0).(5分)
(2)由圆与抛物线的对称性可知抛物线的顶点P的坐标为(1,3);(6分)
∴设抛物线解析式为y=a(x-1)2+3,
由已知得抛物线经过点B(1+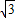 ,0),(7分)
,0),(7分)
把点B(1+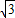 ,0)代入上式,
,0)代入上式,
解得a=-1,(8分)
∴抛物线的解析式为:y=-x2+2x+2.(9分)
(利用抛物线经过P(1,3),A(1-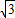 ,0),B(1+
,0),B(1+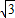 ,0)
,0)
点评:此题考查了垂径定理、勾股定理、抛物线和圆的对称性、二次函数解析式的确定等知识,虽然涉及知识点较多,但难度不大.
(2)根据抛物线和圆的对称性知:C、P都在弦AB的垂直平分线上,已知了C点坐标和圆的半径,即可得到点P的坐标,而P为抛物线顶点,可将所求抛物线设为顶点坐标式,然后将A点坐标代入抛物线的解析式中,即可求得待定系数的值,从而求出该抛物线的解析式.
解答:
 解:(1)过点C作CH⊥x轴,H为垂足;
解:(1)过点C作CH⊥x轴,H为垂足;又∵C(1,1),
∴CH=OH=1;(1分)
∴在Rt△CHB中,
 ;(3分)
;(3分)∵CH⊥AB,CA=CB,
∴AH=BH;
故A(1-
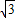 ,0),B(1+
,0),B(1+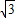 ,0).(5分)
,0).(5分)(2)由圆与抛物线的对称性可知抛物线的顶点P的坐标为(1,3);(6分)
∴设抛物线解析式为y=a(x-1)2+3,
由已知得抛物线经过点B(1+
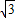 ,0),(7分)
,0),(7分)把点B(1+
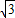 ,0)代入上式,
,0)代入上式,解得a=-1,(8分)
∴抛物线的解析式为:y=-x2+2x+2.(9分)
(利用抛物线经过P(1,3),A(1-
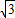 ,0),B(1+
,0),B(1+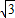 ,0)
,0)点评:此题考查了垂径定理、勾股定理、抛物线和圆的对称性、二次函数解析式的确定等知识,虽然涉及知识点较多,但难度不大.

练习册系列答案
相关题目
 的图象上,若A(13,0)、C(8,2),则k的值为( )
的图象上,若A(13,0)、C(8,2),则k的值为( )