题目内容
已知：如图，AB是半圆O上的直径，E是
的中点，半径OE交弦BC于点D，过点C作⊙O的切线
交OE的延长线于点F．BC=8，DE=2．
（Ⅰ）求⊙O的半径；
（Ⅱ）求点F到⊙O的切线长．
解：（1）∵OE⊥BC，∴CD=
BC=4．
设⊙O半径为r，则OD=r-DE=r-2，
∵CF是⊙O的切线，
∴OC⊥CF，
在Rt△OCD中，有OC2=OD2+CD2，
即r2=（r-2）2+42，解得r=5．
（2）∵∠OCF=∠ODC，∠FOC=∠COD，
∴△OCF∽△ODC，
∴
，∴
．
分析：（1）利用切线的性质，设出半径，再利用勾股定理列出方程即可得出半径；
（2）欲求切线长，只需证明△OCF∽△ODC即可，利用相似三角形的性质即可得出切线CF的长．
点评：本题综合考查了切线的性质和三角形相似的判定及其应用，有一定的难度，要求学生能够仔细读题，把握已知，认真完成题目要求．
BC=4．设⊙O半径为r，则OD=r-DE=r-2，
∵CF是⊙O的切线，
∴OC⊥CF，
在Rt△OCD中，有OC2=OD2+CD2，
即r2=（r-2）2+42，解得r=5．
（2）∵∠OCF=∠ODC，∠FOC=∠COD，
∴△OCF∽△ODC，
∴
，∴．分析：（1）利用切线的性质，设出半径，再利用勾股定理列出方程即可得出半径；
（2）欲求切线长，只需证明△OCF∽△ODC即可，利用相似三角形的性质即可得出切线CF的长．
点评：本题综合考查了切线的性质和三角形相似的判定及其应用，有一定的难度，要求学生能够仔细读题，把握已知，认真完成题目要求．
练习册系列答案
相关题目
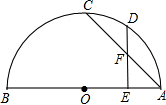已知：如图，AB为⊙O的直径，C、D是半圆弧上的两点，E是AB上除O外的一点，AC与DE相交于F．①
=-
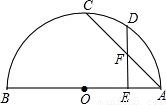
，②DE⊥AB，③AF=DF．
，②DE⊥AB，③AF=DF．
，②DE⊥AB，③AF=DF．